Class 12 Physics Chapter 1 – Electric Charges and Fields
Ans: We are given the following information:
Repulsive force of magnitude,
Charge on the first sphere,
Charge on the second sphere,
Distance between the two spheres,
Electrostatic force between the two spheres is given by Coulomb’s law as,
Where,
Now on substituting the given values, Coulomb’s law becomes,
Therefore, we found the electrostatic force between the given charged spheres to be
2. The electrostatic force on a small sphere of charge
a) What is the distance between the two spheres?
Ans: Electrostatic force on the first sphere is given to be,
Charge of the first sphere is,
Charge of the second sphere is,
We have the electrostatic force given by Coulomb’s law as,
Substituting the given values in the above equation, we get,
Therefore, we found the distance between charged spheres to be
b) What is the force on the second sphere due to the first?
Ans: From Newton’s third law of motion, we know that every action has an equal and opposite reaction.
Thus, we could say that the given two spheres would attract each other with the same force.
So, the force on the second sphere due to the first sphere will be
3. Check whether the ratio
Ans: We are given the ratio,
Here, G is the gravitational constant which has its unit
In the expression for k,
Now, we could find the dimension of the given ratio by considering their units as follows:
Clearly, it is understood that the given ratio is dimensionless.
Now, we know the values for the given physical quantities as,
Substituting these values into the required ratio, we get,
We could infer that the given ratio is the ratio of electrical force to the gravitational force between a proton and an electron when the distance between them is kept constant.
4.
a) Explain the meaning of the statements ‘electric charge of a body is quantized’.
Ans: The given statement ‘Electric charge of a body is quantized’ means that only the integral number
That is, charges cannot be transferred from one body to another in fraction.
b) Why can one ignore quantization of electric charge when dealing with macroscopic i.e., large scale charges?
Ans: On a macroscopic scale or large-scale, the number of charges is as large as the magnitude of an electric charge.
So, quantization is considered insignificant at a macroscopic scale for an electric charge and electric charges are considered continuous.
5. When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Ans: Rubbing two objects would produce charges that are equal in magnitude and opposite in nature on the two bodies.
This happens due to the reason that charges are created in pairs. This phenomenon is called charging by friction.
The net charge of the system however remains zero as the opposite charges equal in magnitude annihilate each other.
So, rubbing a glass rod with a silk cloth creates opposite charges of equal magnitude on both of them and this observation is found to be consistent with the law of conservation of charge.
6. Four point charges
Ans: Consider the square of side length
From the figure we find the diagonals to be,
Now the repulsive force at O due to charge at A,
And the repulsive force at O due to charge at D,
And the attractive force at O due to charge at B,
And the attractive force at O due to charge at C,
We find that (1) and (2) are of same magnitude but they act in the opposite direction and hence they cancel out each other.
Similarly, (3) and (4) are of the same magnitude but in the opposite direction and hence they cancel out each other too.
Hence, the net force on charge at centre O is found to be zero.
7.
a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
Ans: An electrostatic field line is a continuous curve as the charge experiences a continuous force on being placed in an electric field.
As the charge doesn’t jump from one point to the other, field lines will not have sudden breaks.
b) Explain why two field lines never cross each other at any point?
Ans: If two field lines are seen to cross each other at a point, it would imply that the electric field intensity has two different directions at that point, as two different tangents (representing the direction of electric field intensity at that point) can be drawn at the point of intersection.
This is however impossible and thus, two field lines never cross each other.
8. Two point charges
a) What is the electric field at the midpoint O of the line AB joining the two charges?
Ans: The situation could be represented in the following figure. Let O be the midpoint of line AB.
We are given:
Take E to be the electric field at point O, then,
The electric field at point O due to charge
The electric field at point O due to charge
The net electric field,
Therefore, the electric field at mid-point O is
b) If a negative test charge of magnitude
Ans: We have a test charge of magnitude
So, the force experienced by the test charge would be F,
This force will be directed along OA since like charges repel and unlike charges attract.
9. A system has two charges
Ans: The figure given below represents the system mentioned in the question:
The charge at point A,
The charge at point B,
Then, the net charge would be,
The distance between two charges at A and B would be,
The electric dipole moment of the system could be given by,
Therefore, the electric dipole moment of the system is found to be
10. An electric dipole with dipole moment
Ans: We are given the following:
Electric dipole moment,
Angle made by
Electric field,
Torque acting on the dipole is given by
Substituting the given values we get,
Thus, the magnitude of the torque acting on the dipole is found to be
11. A polythene piece rubbed with wool is found to have a negative charge of
a) Estimate the number of electrons transferred (from which to which?)
Ans: When polythene is rubbed against wool, a certain number of electrons get transferred from wool to polythene.
As a result of which wool becomes positively charged on losing electrons and polythene becomes negatively charged on gaining them.
We are given:
Charge on the polythene piece,
Charge of an electron,
Let n be the number of electrons transferred from wool to polythene, then, from the property of quantization we have,
Now, on substituting the given values, we get,
Therefore, the number of electrons transferred from wool to polythene would be
b) Is there a transfer of mass from wool to polythene?
Ans: Yes, during the transfer of electrons from wool to polythene, along with charge, mass is transferred too.
Let
Thus, we found that a negligible amount of mass does get transferred from wool to polythene.
12.
a) Two insulated charged copper spheres
Ans: We are given:
Charges on spheres
Distance between the centres of the spheres is given as,
It is known that the force of repulsion between the two spheres would be given by Coulomb’s law as,
Where,
Substituting the known values into the above expression, we get,
Thus, the mutual force of electrostatic repulsion between the two spheres is found to be
b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?
Ans: It is told that the charges on both the spheres are doubled and the distance between the centres of the spheres is halved. That is,
Now, we could substitute these values in Coulomb’s law to get,
The new mutual force of electrostatic repulsion between the two spheres is found to be
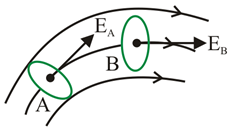
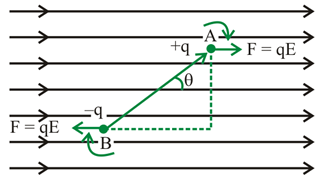
13. Figure below shows tracks taken by three charged particles in a uniform electrostatic field. Give the signs of the three charges and also mention which particle has the highest charge to mass ratio?
Ans: From the known properties of charges, we know that the unlike charges attract and like charges repel each other.
So, the particles 1 and 2 that move towards the positively charged plate while repelling away from the negatively charged plate would be negatively charged and the particle 3 that moves towards the negatively charged plate while repelling away from the positively charged plate would be positively charged.
Now, we know that the charge to mass ratio (which is generally known as emf) is directly proportional to the displacement or the amount of deflection for a given velocity.
Since the deflection of particle 3 is found to be maximum among the three, it would have the highest charge to mass ratio.
14. Consider a uniform electric field
a) Find the flux of this field through a square of side
Ans: We are given:
Electric field intensity,
Magnitude of electric field intensity,
Side of the square,
Area of the square,
Since the plane of the square is parallel to the y-z plane, the normal to its plane would be directed in the x direction. So, angle between normal to the plane and the electric field would be,
We know that the flux through a surface is given by the relation,
Substituting the given values, we get,
Thus, we found the net flux through the given surface to be
b) What would be the flux through the same square if the normal to its plane makes
Ans: When the plane makes an angle of
So, we found the flux in this case to be,
15. What is the net flux of the uniform electric field of exercise
Ans: We are given that all the faces of the cube are parallel to the coordinate planes.
Clearly, the number of field lines entering the cube is equal to the number of field lines entering out of the cube. As a result, the net flux through the cube would be zero.
16. Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is
a) What is the net charge inside the box?
Ans: We are given that:
Net outward flux through surface of the box,
For a body containing of net charge
Where,
Therefore, the charge
Therefore, the net charge inside the box is found to be
b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or why not?
Ans: No, the net flux entering out through a body depends on the net charge contained within the body according to Gauss’s law.
So, if the net flux is given to be zero, then it can be inferred that the net charge inside the body is zero.
However, the net charge of the body being zero only implies that the body has equal amount of positive and negative charges and thus, we cannot conclude that there were no charges inside the box.
17. A point charge
Ans: Consider the square as one face of a cube of edge length
The electric flux through one face of the cube could be now given by,
The net charge enclosed would be,
Substituting the values given in the question, we get,
Therefore, electric flux through the square is found to be
18. A point charge of
Ans: Let us consider one of the faces of the cubical Gaussian surface considered (square).
Since a cube has six such square faces in total, we could say that the flux through one surface would be one-sixth the total flux through the gaussian surface considered.
The net flux through the cubical Gaussian surface by Gauss’s law could be given by,
So, the electric flux through one face of the cube would be,
But we have,
Charge enclosed,
Substituting the given values in (1) we get,
Therefore, electric flux through the square surface is
19. A point charge causes an electric flux of
a) If the radius of the Gaussian surface were doubled, how much flux could pass through the surface?
Ans: We are given:
Electric flux due to the given point charge,
Radius of the Gaussian surface enclosing the point charge,
Electric flux piercing out through a surface depends on the net charge enclosed by the surface according to Gauss’s law and is independent of the dimensions of the arbitrary surface assumed to enclose this charge.
Hence, if the radius of the Gaussian surface is doubled, then the flux passing through the surface remains the same i.e.,
b) What is the magnitude of the point charge?
Ans: Electric flux could be given by the relation,
Where,
Substituting the given values,
Thus, the value of the point charge is found to be
20. A conducting sphere of radius
Ans: We have the relation for electric field intensity
Where,
Net charge,
Distance from the centre,
From (1), the unknown charge would be,
Substituting the given values we get,
Therefore, the net charge on the sphere is found to be
21. A uniformly charged conducting sphere of
a) Find the charge on the sphere.
Ans: Given that,
Diameter of the sphere,
Radius of the sphere,
Surface charge density,
Total charge on the surface of the sphere,
Therefore, the charge on the sphere is found to be
b) What is the total electric flux leaving the surface of the sphere?
Ans: Total electric flux
Where, permittivity of free space,
We found the charge on the sphere to be,
Substituting these in (1), we get,
Therefore, the total electric flux leaving the surface of the sphere is found to be
22. An infinite line charge produces a field of magnitude
Ans: Electric field produced by the given infinite line charge at a distance
We are given:
Permittivity of free space,
Substituting these values in (1) we get,
Therefore, we found the linear charge density to be
23. Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude
Ans: The given nature of metal plates is represented in the figure below:
Here, A and B are two parallel plates kept close to each other. The outer region of plate A is denoted as
It is given that:
Charge density of plate A,
Charge density of plate B,
In the regions
Now, the electric field
Where,
Permittivity of free space
Clearly,
Thus, the electric field between the plates is
List of Important Formulas in Class 12 Physics Chapter 1 Electric Charges And Fields
While preparing a chapter, it is important for students to memorize the formula of a particular topic. This will help them to boost their score. Some important formulas are listed below.
Coulomb’s Law
The electric force between the two-point charges are directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
F = K
Here,
F represents the electric force.
K represents Coulomb’s constant.
q1q2 represents the two charges.
Electric field intensity
Electric field intensity is the vector quantity.
E
Fq1
Here,
F is the force experienced by the test charge.
q1 is the test charge.
Electric Flux
dФ = E.da
dФ = E.da cos𝛉
Ф = ഽ E.da
Chapter Summary of Electric Charges & Fields NCERT Solutions
From simple experiments on frictional electricity, one can infer that there are two types of charges in nature; and that like charges repel and unlike charges attract. By convention, the charge on a glass rod rubbed with silk is positive; that on a plastic rod rubbed with fur is then negative.
Charge is not only a scalar (or invariant) under rotation; it is also invariant for frames of reference in relative motion. This is not always true for every scalar. For Example-, kinetic energy is a scalar under rotation, but is not invariant for frames of reference in relative motion.
Conductors allow movement of electric charge through them, insulators do not. In metals, the mobile charges are electrons; in electrolytes both positive and negative ions are mobile.
Coulomb’s Law: The mutual electrostatic force between two point charges q1 and q2 is proportional to the product q1q2 and inversely proportional to the square of the distance r21 separating them.
Where
In SI units, the unit of charge is coulomb. The experimental value of the constant
The approximate value of k is- 9\times
Superposition Principle: The principle is based on the property that the forces with which two charges attract or repel each other are not affected by the presence of a third (or more) additional charge(s). For an assembly of charges Q1, Q2, Q3..., the force on any charge, say Q1, is the vector sum of the force on Q1 due to Q2, the force on Q1 due to Q3, and so on. For each pair, the force is given by Coulomb's law for two charges stated earlier.
An electric field line is a curve drawn in such a way that the tangent at each point on the curve gives the direction of the electric field at that point. The relative closeness of field lines indicates the relative strength of electric field at different points; they crowd near each other in regions of strong electric field and are far apart where the electric field is weak. In regions of constant electric field, the field lines are uniformly spaced parallel straight lines.
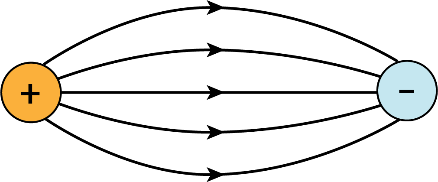
Some of the important properties of field lines are: (i) Field lines are continuous curves without any breaks. (ii) Two field lines cannot cross each other. (iii) Electrostatic field lines start at positive charges and end at negative charges (iv) They cannot form closed loops.
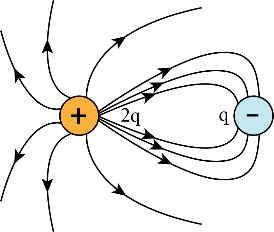
Electric flux is the measure of the field lines crossing a surface. It is scalar quantity, with SI unit
NC -m2 or V-m. “The number of field lines passing through perpendicular unit area will be proportional to the magnitude of Electric Field there”Gauss’s law: The flux of electric field through any closed surface S is
1/ε0 times the total charge enclosed by S. The law is especially useful in determining electric field E, when the source distribution has simple symmetry.An electric dipole is a pair of equal and opposite charges q and –q separated by some distance 2a. Its dipole moment vector p has magnitude 2qa and is in the direction of the dipole axis from –q to q.
Field of an electric dipole in its equatorial plane (i.e., the plane perpendicular to its axis and passing through its centre) at a distance r from the centre:
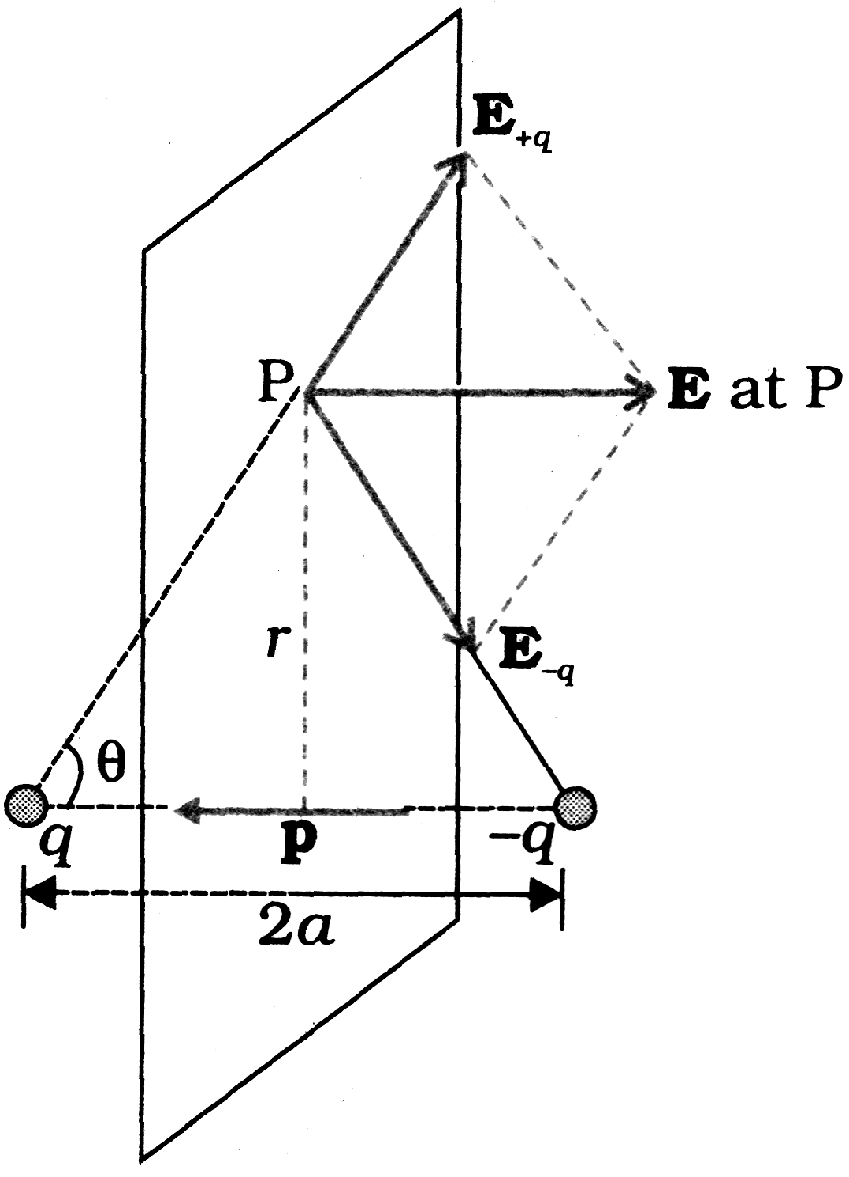
Dipole electric field on the axis at a distance r from the centre:

The 1/r3 dependence of dipole electric fields should be noted in contrast to the 1/r2 dependence of electric field due to a point charge.
In a uniform electric field E, a dipole experiences a torque τ given by: τ = p × E
but experiences no net force.
Electric Field Due to Various Uniform Charge Distribution
(i) At the centre of circular arc  | |
(ii) At a point on the axis of ring 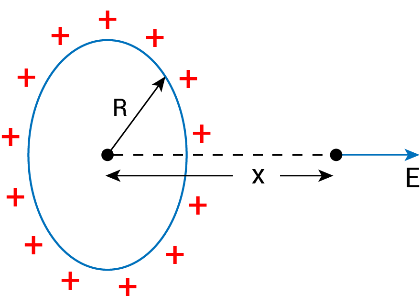 | 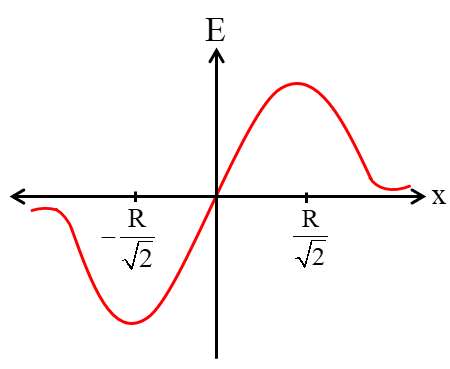 |
(iii) At a point on the axis of disc 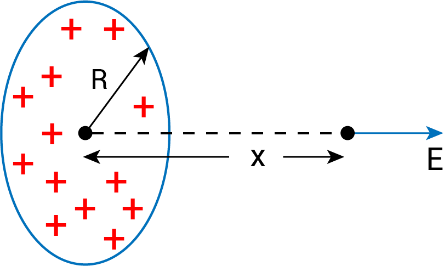 | |
(iv) Hollow sphere 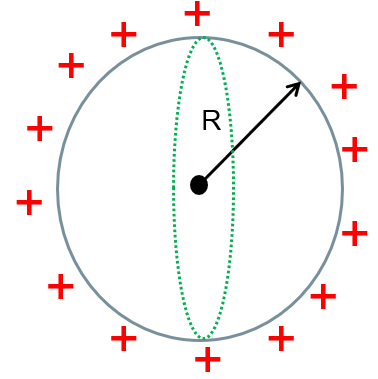 | For x < R: E = 0 For x ≥ R: 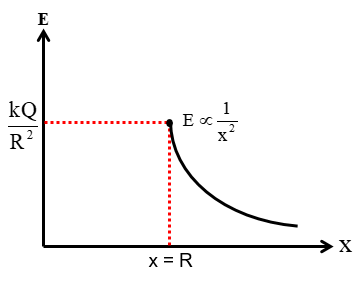 |
(v) Non conducting solid sphere  | For x < R: For x ≥ R: 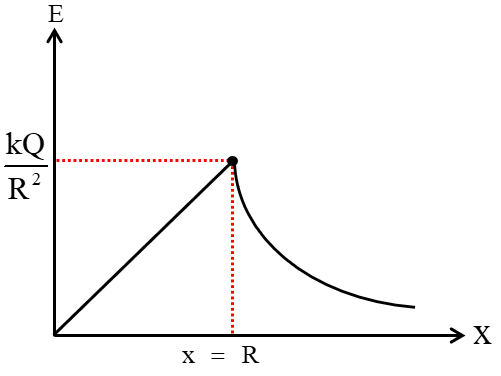 |
(vi) Infinite thin sheet 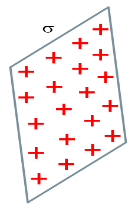 | |
(vii) Infinite wire 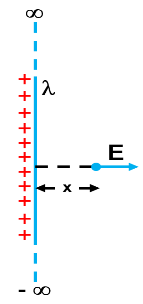 |

0 Comments