GSEB Std 12 Physics MCQ Chapter 10 તરંગ પ્રકાશશાસ્ત્ર in Gujarati Medium
પ્રશ્ન 1.
પ્રકાશના ન્યૂટનના કણવાદ અનુસાર પ્રકાશની ઝડપ …………………………… હોય છે.
(A) પાતળા માધ્યમમાં વધારે અને ઘટ્ટ માધ્યમમાં ઓછી
(B) પાતળા માધ્યમમાં ઓછી અને ઘટ્ટ માધ્યમમાં વધારે
(C) બંને માધ્યમમાં સમાન
(D) આમાંથી એક પણ નહીંg
જવાબ
(B) પાતળા માધ્યમમાં ઓછી અને ઘટ્ટ માધ્યમમાં વધારે
પ્રશ્ન 2.
પ્રકાશ સીધી લીટીમાં ગતિ કરે છે. કારણ કે, …………………….
(A) તેમનો વેગ ઘણો મોટો છે.
(B) તે આસપાસમાં શોષાતો નથી.
(C) તેની તરંગલંબાઈ ઘણી જ નાની છે.
(D) તે આસપાસથી પરાવર્તિત થતો નથી.
જવાબ
(C) તેની તરંગલંબાઈ ઘણી જ નાની છે.
પ્રશ્ન 3.
પ્રકાશના પ્રસરણ માટેનો તરંગવાદ ……………………… નામના વૈજ્ઞાનિકે આપ્યો.
(A) ન્યૂટન
(B) મૅક્સવેલ
(C) હાઇગેન્સ
(D) ડેકાર્ટિસ
જવાબ
(C) હાઇગેન્સ
પ્રશ્ન 4.
એક જ તરંગઅગ્ર પર રહેલાં બધા જ કણો માટે ……………………. હોય છે.
(A) કળા શૂન્ય
(B) કળા જુદી-જુદી
(D) કળા 2 રેડિયન જેટલી જ
(C) કળા સમાન
જવાબ
(C) કળા સમાન
પ્રશ્ન 5.
એક જ તરંગઅગ્ર પર λ અંતરે રહેલા બે કણોના દોલનોની કળા વચ્ચે કળાનો તફાવત ………………….. હોય છે.
(A) હંમેશાં શૂન્ય
(B) અન્વનર
(C) હંમેશાં
(D) હંમેશાં 2π રેડિયન જેટલો
જવાબ
(A) હંમેશાં શૂન્ય
પ્રશ્ન 6.
તરંગઅગ્રને લંબ અને તરંગના પ્રસરણની દિશા દર્શાવતી રેખાને ………………………. કહે છે.
(A) તરંગરેખા
(C) કિરણ
(B) માત્ર સુરેખા
(D) તરંગ
જવાબ
(C) કિરણ
પ્રશ્ન 7.
હાઇગેન્સનો તરંગવાદનો સૌથી અગત્યનો મુદ્દો ……………………. છે.
(A) માત્ર યાંત્રિક તરંગોને લાગુ પડે
(B) માત્ર બિનયાંત્રિક તરંગોને લાગુ પડે
(C) માત્ર સંગત તરંગોને લાગુ પડે
(D) બધા જ પ્રકારના તરંગોને લાગુ પડે
જવાબ
(D) બધા જ પ્રકારના તરંગોને લાગુ પડે
પ્રશ્ન 8.
હાઇગેન્સના સિદ્ધાંત પરથી પ્રકાશ એ …………………… સ્વરૂપે છે.
(A) કણ
(C) તરંગ
(B) કિરણો
(D) આમાંથી એક પણ નહીં
જવાબ
(C) તરંગ
પ્રશ્ન 9.
બિંદુવત્ ઉદ્ગમમાંથી ઉદ્ભવતા અને સમાંગ તથા સમદિગ્ધર્મી માધ્યમમાં ત્રિપરિમાણમાં પ્રસરતા તરંગોના તરંગઅગ્રનો આકાર ………………….. હોય છે.
(A) સમતલ
(B) ગોળાકાર
(C) નળાકાર
(D) અનિયમિત
જવાબ
(B) ગોળાકાર
પ્રશ્ન 10.
શાંત પાણીમાં પથ્થર નાંખતા રચાતા તરંગઅગ્રોનો આકાર ……………………. હોય છે.
(A) સમતલ
(B) ગોળાકાર
(C) નળાકાર
(D)અનિયમિત
જવાબ
(B) ગોળાકાર
પ્રશ્ન 11.
અનંત અંતરે જતાં ગોળાકાર તરંગો …………………… બને છે.
(A) સમતલ
(B) નળાકાર
(C) અનિયમિત
(D) કિરણ
જવાબ
(A) સમતલ
પ્રશ્ન 12.
હાઇગેન્સના સિદ્ધાંતની મર્યાદાની સમજૂતી …………………….. નામના વૈજ્ઞાનિકોએ આપી.
(A) હાઇગેન્સ અને રેલે
(B) વાયોગ્ય અને કિર્ચીફ
(C) ફ્રેનલ અને ફ્રોનહૉફર
(D) માલસ અને યંગ
જવાબ
(B) વાયોગ્ય અને કિર્ચીફ
પ્રશ્ન 13.
ગૌણ તરંગોની તીવ્રતા ……………………. પદના સમપ્રમાણમાં છે.
(A) sin2θ
(B) sin2(
(C) cos2θ
(D) cos2(
જવાબ
(D) cos2(
પ્રશ્ન 14.
હાઇગેન્સનો તરંગવાદ ………………………… ઘટના સમજાવી શકતો નથી
(A) વિવર્તન
(B) વ્યતિકરણ
(C) ધ્રુવીભવન
(D) ફોટોઇલેક્ટ્રિક અસર
જવાબ
(D) ફોટોઇલેકિટ્રક અસર
પ્રશ્ન 15.
કોઈ પણ તરંગના ક્રમિક શૃંગ અને ગર્ત વચ્ચેનો કળા-તફાવત …………………….. હોય છે.
(A)
(B) π
(C) 2π
(D) શૂન્ય
જવાબ
(A)
પ્રશ્ન 16.
પાતળા માધ્યમમાં પ્રકાશનો વેગ v1 છે, તે ઘટ્ટ માધ્યમમાં i આપાતકોણે આપાત થઈ પસાર થાય ત્યારે તેનો વેગ v2
બને અને વક્રીભૂતકોણ r હોય, તો …………………….
(A) v1 = v2
(B) v1 > v2
(C) v1 < v2
(D) આમાંથી એક પણ નહીં
જવાબ
(B) v1 > v2
સ્નેલના નિયમ અનુસાર,
અહીં વક્રીભૂતકિરણ લંબની નજીક વાંકુ વળે છે તેથી,
r < i ∴
∴
∴ v1 > v2
પ્રશ્ન 17.
કાચનો વક્રીભવનાંક 1.9 છે. જો તેં જાડાઇના કાચના સ્લેબમાંથી પસાર થતાં
લાગતો સમય t છે અને 1.5 d લેવલ સુધી પારદર્શક બીકરમાં ભરેલાં પાણીમાંથી
પસાર થતાં લાગતો સમય સમાન છે, તો પાણીનો વક્રીભવનાંક ………………………
(A) 1.27
(B) 1.33
(C) 1.20
(D) 1.50
જવાબ
(A) 1.27
µ1L1 = µ2L2
∴ µ2 =
=
= 1.26666
≈ 1.27
પ્રશ્ન 18.
1.5 વક્રીભવનાંકવાળા કાચના 2 cm જાડાઇના સ્લેબમાંથી જેટલાં સમયમાં પ્રકાશ
પસાર થાય છે તેટલાં જ સમયમાં 2.25 cm ના માધ્યમમાં પસાર થાય છે, તો
માધ્યમનો વક્રીભવનાંક ……………………..
(A)
(B)
(C)
(D)
જવાબ
(A)
આપેલા સમાન સમયમાં પ્રકાશીય પથ સમાન,
µ1x1 = µ2x2
µ2 =
પ્રશ્ન 19.
પરાવર્તક સમતલ સપાટી પર 5000 Å તરંગલંબાઈનો પ્રકાશ આપાત થાય છે, તો
આપાતકોણના ………………….. ખૂણા માટે પરાવર્તિત કિરણ અને આપાતકિરણ લંબ થશે.
(A) 0°
(B) 30°
(C) 90°
(D) 45°
જવાબ
(D) 45°
અહીં i + r = 90°
પણ i = r માટે 2i = 90°
∴ i = 45°
પ્રશ્ન 20.
ચોક્કસ રંગના હવામાં 1 mm અંતરમાં 2000 તરંગો આવેલાં છે, તો 1.25 વક્રીભવનાંકવાળા માધ્યમમાં પ્રકાશની તરંગલંબાઈ કેટલી ?
(A) 1000 Å
(B) 2000 Å
(C) 3000 Å
(D) 4000 Å
જવાબ
(D) 4000 Å
λહવા =
λમાધ્યમ =  = 4000 Å
= 4000 Å
પ્રશ્ન 21.
એક તારા (Star)માંથી ઉત્સર્જિત પ્રકાશની તરંગલંબાઈ જાંબલી રંગ તરફ ખસે છે, તો આ તારો ………………………..
(A) સ્થિર હશે.
(B) પૃથ્વી તરફ ગતિ કરતો હશે.
(C) પૃથ્વીથી દૂર જતો હશે.
(D) માહિતી અપૂર્ણ છે.
જવાબ
(B) પૃથ્વી તરફ ગતિ કરતો હશે.
તરંગલંબાઈ જાંબલી રંગ તરફ ખસે છે એટલે કે, તરંગલંબાઈ ઘટે છે. તેથી, તારો (ઉદ્ગમ) પૃથ્વી તરફ ગતિ કરે છે.
પ્રશ્ન 22.
એક રૉકેટ 6 × 10-7m/sની ઝડપથી પૃથ્વીથી દૂર જાય છે અને તેની
અંદર વાદળી પ્રકાશ છે, તો પૃથ્વી પર રહેલાં અવલોકનકાર તે પ્રકાશની
તરંગલંબાઈ કેટલી અનુભવાશે ? વાદળી પ્રકાશની તરંગલંબાઈ = 4600 Å છે.
(A) 4600 Å
(B) 5520 Å
(C) 3680 Å
(D) 3920 Å
જવાબ
(B) 5520 Å
∴ Δλ = λ’ – λ
∴ 0.2λ = λ’ – λ
∴ λ’ = 1.20
= 1.2 × 4600 Å
∴ λ’ = 5520 Å
પ્રશ્ન 23.
દૂરના તારામાંથી આવતાં 5000 Å તરંગલંબાઈવાળા તરંગની તરંગલંબાઈ 5200 Å અનુભવાય છે, તો પાછા ફરતાં તારનો વેગ કેટલો ?
(A) 1.2 × 107 cm/s
(B) 1.2 × 107 m/s
(C) 1.2 × 107 km/s
(D) 1.2 km/s
જવાબ
(B) 1.2 × 107m/s
અહીં Δλ = λ’ – λ
= 5200 – 5000
= 200 Å
હવે
∴ v = 1.2 × 107 m/s
પ્રશ્ન 24.
કોઈ એક પ્રકાશનું ઉદ્ગમ અવલોકનકાર તરફ ગતિ કરતું હોય તો ……………………….
(A) પ્રકાશની ઝડપ વધશે.
(B) પ્રકાશની તરંગલંબાઈ બદલાશે નહીં.
(C) પ્રકાશની તરંગલંબાઈ વધશે.
(D) પ્રકાશની તરંગલંબાઈ ઘટશે.
જવાબ
(D) પ્રકાશની તરંગલંબાઈ ઘટશે.
ડૉપ્લર અસર પરથી પ્રકાશનું ઉદ્ગમ સ્થિર અવલોકનકાર તરફ ગતિ કરે તો અવલોકનકારને અનુભવાતી આવૃત્તિ
fL = (
જ્યાં v = શૂન્યાવકાશમાં પ્રકાશનો વેગ
vs = ઉદ્ગમનો વેગ
fs= ઉદ્ગમમાંથી ઉત્સર્જાતા પ્રકાશની આવૃત્તિ
∴ fL > fs [∵
અને
∴ λs > λL
∴ અવલોકનકારને અનુભવાતી તરંગલંબાઈ λL, ઘટશે.
પ્રશ્ન 25.
સ્થિર અવલોકનકારથી દૂર પ્રકાશનું ઉદ્ગમ જઈ રહ્યું હોય તો આપેલ પ્રકાશની આવૃત્તિ બદલાય છે, તે ………………………. ઘટના વડે સમજાવી શકાય.
(A) ડૉપ્લર અસર
(B) વ્યતિકરણ
(C) વિવર્તન
(D) એક પણ નહીં.
જવાબ
(A) ડૉપ્ટર અસર
પ્રશ્ન 26.
એક તારો પૃથ્વીથી 100 kms-1 ના વેગથી દૂર થાય છે. જો પ્રકાશની ઝડપ 3 × 108 ms-1 હોય તો 5700 Å તરંગલંબાઈના વર્ણપટ રેખાની ડોપ્લર શિફ્ટ શોધો.
(A) 0.63 Å
(B) 1.90 Å
(C) 3.80 Å
(D) 5.70 Å
જવાબ
(B) 1.90 Å

પ્રશ્ન 27.
સ્રોત Sમાંથી ઉત્સર્જાતા પ્રકાશનો Sની સાપેક્ષે વેગ c છે. જો અવલોકનકાર O એ
S તરફ v વેગથી ગતિ કરે, તો અવલોકનકારને । અનુભવાતા પ્રકાશનો વેગ ……………………
(A) c + v
(B) c – v
(C) c
(D)
જવાબ
(C) c
પ્રશ્ન 28.
પ્રકાશની ડોપ્લર અસરમાં પદ રેડ શિફ્ટ’ દર્શાવે છે, કે ………………………
(A) આવૃત્તિમાં ઘટાડો
(B) આવૃત્તિમાં વધારો
(C) તીવ્રતામાં ઘટાડો
(D) તીવ્રતામાં વધારો
જવાબ
(A) આવૃત્તિમાં ઘટાડો
પ્રશ્ન 29.
એક તારામાંથી ઉત્સર્જિત 5000 Å ની તરંગલંબાઈવાળું વિકિરણ પૃથ્વી પર પહોંચતા વેગ 1.5 × 106m/s છે, તો પૃથ્વી પર પહોંચતા વિકિરણની તરંગલંબાઈમાં ફેરફાર ………………………
(A) 25 Å
(B) શૂન્ય
(C) 100Å
(D) 2.5 Å
જવાબ
(A) 25 Å
Δλ = λ ×
= 5000 ×
= 25 Å
પ્રશ્ન 30.
જ્યારે તારો પૃથ્વીથી 0.8ની ઝડપથી દૂર જાય ત્યારે તે 6 × 1014 Hz આવૃત્તિવાળો પ્રકાશ ઉત્સર્જિત કરે છે, તો પૃથ્વી પર કેટલાં 1014Hzમાં આવૃત્તિ અનુભવાશે ? (c = 3 × 108m/s)
(A) 0.24
(B) 1.2
(C) 30
(D) 3.3
જવાબ
(B) 1.2
અનુભવાતી આવૃત્તિ,
v’ = v(1 –
= 6 × 1014(1 –
= 6 × 1014 (1 – 0.8)
= 6 × 1014 × 0.2
= 1.2 × 1014 ∴ વિકલ્પ 1.2
પ્રશ્ન 31.
માધ્યમના કોઈ ચોક્કસ બિંદુ આગળ બે કરતાં વધારે તરંગોના સંપાતીકરણને લીધે ઉદ્ભવતી ભૌતિક અસરને ……………………. કહે છે.
(A) પરાવર્તન
(B) વક્રીભવન
(C) વ્યતિકરણ
(D) વિવર્તન
જવાબ
(C) વ્યતિકરણ
પ્રશ્ન 32.
નીચેનામાંથી કયા તરંગોમાં વ્યતિકરણ મળી શકે ?
(A) લંબગત
(C) વિદ્યુતચુંબકીય
(B) સંગત
(D) ઉપરના બધા જ
જવાબ
(D) ઉપરના બધા જ
પ્રશ્ન 33.
વ્યતિકરણની ઘટનાનું નિર્દશન કરવા આપણે બે એવા ઉદ્ગમોની જરૂર પડે છે, કે જે ઉત્સર્જાતા વિકિરણની ……………………
(A) લગભગ આવૃત્તિ સમાન હોય.
(B) સમાન આવૃત્તિ હોય.
(C) જુદી-જુદી તરંગલંબાઈ હોય.
(D) સમાન આવૃત્તિ અને ચોક્કસ કળાતફાવત હોય.
જવાબ
(D) સમાન આવૃત્તિ અને ચોક્કસ કળાતફાવત હોય.
પ્રશ્ન 34.
બે પ્રકાશ તરંગોના સ્થાનાંતરો e1 = 4sin ωt અને e2 = 3 sin (ωt +
(A) 0
(B) 1
(C) 5
(D) 7
જવાબ
(C) 5
અહીં E1 = 4 અને E2 = 3 તથા કળા-તફાવત =
પરિણામી તરંગનો કંપવિસ્તાર,

∴ E = 5 એકમ
પ્રશ્ન 35.
પ્રકાશના તરંગની તીવ્રતા I તેના
(A) વર્ગના વ્યસ્ત
(B) ચતુર્થ ઘાતના સમ
(C) ચતુર્થ ઘાતના વ્યસ્ત
(D) વર્ગના સમ
જવાબ
(D) વર્ગના સમ
પ્રશ્ન 36.
તરંગનો કંપવિસ્તાર 3 ગણો કરતાં તરંગની તીવ્રતા ……………………. થાય.
(A) √3 ગણી
(B) 3 ગણી
(C) 9 ગણી
(D)
જવાબ
(C) 9 ગણી
તીવ્રતા I ∞ (કંપવિસ્તાર E)2
∴
∴ I2 = I1 ×
પ્રશ્ન 37.
સ્થિત વ્યતિકરણ માટેની સૌથી અગત્યની શરત એ છે, કે ઉદ્ગમો …………………….. હોવાં જોઈએ.
(A) સુસંબદ્ધ
(B) અસુસંબદ્ધ
(C) મોટા પરિમાણવાળા
(D) સ્થિર
જવાબ
(A) સુસંબદ્ધ
પ્રશ્ન 38.
બે તરંગોની તીવ્રતાનો ગુણોત્તર 1 : 9 છે. જો આ તરંગનું વ્યતિકરણ થાય તો મહત્તમ અને લઘુતમ તીવ્રતાનો ગુણોત્તર જણાવો. (AIIMS – 2000)
(A) 3 : 1
(B) 4 : 1
(C) 9 : 1
(D) 16 : 1
જવાબ
(B) 4 : 1
I ∝ A2

પ્રશ્ન 39.
બે સુસમ્બદ્ધ તરંગોના કંપવિસ્તારનો ગુણોત્તર 5 : 2 છે. તેમનાથી ઉદ્ભવતી
સ્થિત વ્યતિકરણ ભાત માટે સહાયક અને વિનાશક વ્યતિકરણ માટેની શલાકાઓની
તીવ્રતાનો
ગુણોત્તર ………………… છે.
(A)
(B)
(C)
(D)
જવાબ
(A)
∴
=
∴
પ્રશ્ન 40.
બે સુસમ્બદ્ધ ઉદ્ગમોની તીવ્રતા ભિન્ન છે અને તેમાંથી ઉત્સર્જિત થતા
તરંગોનું વ્યતિકરણ થાય છે. વ્યતિકરણમાં મહત્તમ અને ન્યૂનતમ તીવ્રતાઓનો
ગુણોત્તર 25 છે. તો ઉદ્ગમની તીવ્રતાઓનો ગુણોત્તર …………………. (GUJCET – 2007)
(A) 5 : 1
(B) 9 : 4
(C) 25 : 16
(D) 25 : 1
જવાબ
(B) 9 : 4

પ્રશ્ન 41.
યંગના પ્રયોગમાં વ્યતિકરણ શલાકાઓની મહત્તમ અને લઘુતમ તીવ્રતાઓનો ગુણોત્તર 9
: 1 છે, તો સંપાત થતા તરંગોના કંપવિસ્તારનો ગુણોત્તર ………………… (GUJCET –
2008)
(A) 9 : 1
(B) 3 : 1
(C) 2 : 1
(D) 1 : 1
જવાબ
(C) 2 : 1

પ્રશ્ન 42.
જો બંને ઉદ્ગમોના દોલનની કળા સમાન હોય અને કળાનો તફાવત અચળ જળવાઈ રહેતો હોય, તો તેવાં ઉદ્ગમોને ………………….. કહે છે.
(A) અશુદ્ધ ઉદ્ગમો
(B) સુસંબદ્ધ ઉદ્ગમો
(C) વિરોધી ઉદ્ગમો
(D) અસુસંબદ્ધ ઉદ્ગમો
જવાબ
(B) સુસંબદ્ધ ઉદ્ગમો
પ્રશ્ન 43.
કયા પ્રકારના ઉદ્ગમોમાં બે ઉદ્ગમોના દોલનની કળાનો તફાવત શૂન્ય થાય ?
(A) અશુદ્ધ ઉદ્ગમો
(B) સુસંબદ્ધ ઉદ્ગમો
(C) વિરોધી ઉદ્ગમો
(D) અસુસંબદ્ધ ઉદ્ગમો
જવાબ
(B) સુસંબદ્ધ ઉદ્ગમો
પ્રશ્ન 44.
નીચે આપેલા સૂત્રો પૈકી સાચું સૂત્ર પસંદ કરો.
(A) કળાનો તફાવત = તરંગ સદિશ × પથતફાવત
(B) કળાનો તફાવત = 
(C) કળાનો તફાવત = 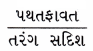
(D) કળાનો તફાવત = 2π × પથતફાવત
જવાબ
(A) કળાનો તફાવત તરંગ સદિશ × પથતફાવત
[ΔΦ = kx]
પ્રશ્ન 45.
સહાયક વ્યતિકરણ માટે કળાના પદમાં શરત ………………………..
(A) કળા તફાવત = nπ, જ્યાં n = 0, 1, 2, 3,
(B) કળા તફાવત = 2nπ, જ્યાં n = 0, 1, 2, 3,
(C) કળા તફાવત = (2n – 1)π, જ્યાં n = 0, 1, 2, 3,
(D) કળા તફાવત = (2n + 1)π, જ્યાં n = 0, 1, 2, 3, ….
જવાબ
(B) કળા તફાવત = 2nπ, જ્યાં n = 0, 1, 2, 3, …
પ્રશ્ન 46.
વિનાશક વ્યતિકરણની કળાના પદમાં શરત …………………
જ્યાં n = 0, 1, 2, 3, ………..
(A) કળા તફાવત = 2nπ
(B) કળા તફાવત = (2n – 1)π
(C) કળા તફાવત = (2n + 1)
(D) કળા તફાવત = (2n + 1)
જવાબ
(C) કળા તફાવત = (2n + 1)π
પ્રશ્ન 47.
સહાયક વ્યતિકરણની પથતફાવતના પદમાં શરત ………………….
જ્યાં n = 0, 1, 2, 3, ……….
(A) પથતફાવત = 2nλ
(B) પથતફાવત = (n +
(C) પથતફાવત = nλ
(D) પથતફાવત = (n –
જવાબ
(C) પથતફાવત = nλ
પ્રશ્ન 48.
વિનાશક વ્યતિકરણની પ્રથતફાવતના પદમાં શરત ………………..
જ્યાં n = 0, 1, 2, 3, ………………
(A) પથતફાવત = nλ
(B) પથતફાવત = (n +
(C) પથતફાવત = 2nλ
(D) પથતફાવત = (2n + 1)λ
જવાબ
(B) પથતફાવત = (n +
પ્રશ્ન 49.
ઉદ્ભવસ્થાન અને પડદા વચ્ચેનું અંતર 2% વધે તો પડદા પર મળતી પ્રકાશની તીવ્રતા ………………….
(A) 4 % જેટલી વધશે.
(B) 2 % જેટલી વધશે.
(C) 2 % જેટલી ઘટશે.
(D) 4% જેટલી ઘટશે.
જવાબ
(D) 4 % જેટલી ઘટશે.
પ્રકાશની તીવ્રતા I =

પ્રશ્ન 50.
સમાન આવૃત્તિ અને સમાન કંપવિસ્તારવાળા બે તરંગોના સંપાતીકરણના લીધે તેટલા કંપવિસ્તારવાળા તરંગો વચ્ચેનો કળા તફાવત ………………..
(A) 30°
(B) 45°
(C) 60°
(D) 120°
(D) 120°
E2 =
પ્રણ E1 = E2 = E
∴ E2 = 2E2 + 2E2cos (δ2 – δ1)
∴ E2 = 2E2(1 + cos(δ2 – δ1)
∴
∴ –
પ્રશ્ન 51.
કોઈ એક બિંદુએ બે વિદ્યુતચુંબકીય તરંગો કોઈ એક ક્ષણે (0, 0, 1) Vm-1 અને (−1, 0, 1) Vm-1 ના સ્થાનાંતરો ઉત્પન્ન કરે છે. તો આ બિંદુએ પરિણામી તીવ્રતા …………………. Wm-2 છે.
(A) √5
(B) 17
(C) 1
(D) 5
જવાબ
(D) 5
= (0, 0, 1) + (-1, 0, 1)
= (-1, 0, 2)
∴ e2 = (-1)2 + (0)2 + (2)2 = 1 + 4 = 5
અને I ∝ e2
∴ I = ke2
∴ I = 1 × 5
∴ I = 5 Wm-2
પ્રશ્ન 52.
પ્રકાશના બે સુસમ્બદ્ધ ઉદ્ગમોની તીવ્રતાઓનો ગુણોત્તર β છે. વ્યતિકરણથી મળતી શલાકાની દૃશ્યતા ……………………… થશે.
(A) 2β
(B)
(C)
(D)
જવાબ
(D)
Imax = I1 + I2 + 2
Imin = I1 – I2 – 2
Imax – Imin = 4
Imax + Imin = 2(I1 + I2)
શલાકાની દૃશ્યતા એટલે

પ્રશ્ન 53.
યંગના પ્રયોગમાં મળતી વ્યતિકરણભાતમાં પ્રકાશની તીવ્રતા 5 એકમ અને અપ્રકાશિત
શલાકાની તીવ્રતા 3 એકમ છે, તો શલાકાની દૃશ્યતા (Visibility) ………………. થશે.
(A) 0.50
(B) 0.75
(C) 1.0
(D) 0.25
જવાબ
(D) 0.25
દશ્યતા =
પ્રશ્ન 54.
સમાન તીવ્રતા I0 ધરાવતા ‘n’ સુસમ્બદ્ધ તરંગોના સંપાતીકરણને લીધે મળતી મહત્તમ તીવ્રતા …………………
(A) nI
(B)
(C) n2I
(D)
જવાબ
(C) n2I

પ્રશ્ન 55.
સમાન તીવ્રતાવાળા બે સુસમ્બદ્ધ પ્રકાશના ઉદ્ગમોમાંથી ઉદ્ભવતા પ્રકાશ તરંગો
વ્યતિકરણ રચે છે. જો ન્યૂનતમ માટે તીવ્રતા શૂન્ય હોય તો મહત્તમ માટે
તીવ્રતા કેટલી ? (AIIMS – 2011)
(A) 4I
(B) I
(C) 4I2
(D) I2
જવાબ
(A) 4I

પ્રશ્ન 56.
આકૃતિમાં દર્શાવ્યા મુજબ મોટી ત્રિજ્યાના વર્તુળના કેન્દ્રની બંને બાજુએ સરખા અંતરે બિંદુવત્ સુસમ્બદ્ધ ઉદ્ગમસ્થાન S1 અને S2
રાખેલ છે. જ્યાં d = 2λ, જ્યાં λ = ઉત્સર્જિત પ્રકાશની તરંગલંબાઈ, તો
મહત્તમ તીવ્રતાના સ્થાન માટે ઉપરના અર્ધવર્તુળ માટે શક્ય θ નાં મૂલ્યો
શોધો.
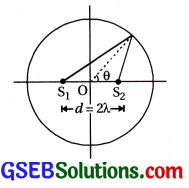
(A) 20°, 50°, 150°
(B) 30, 80°, 120°
(C) 45°, 90°, 170°
(D) 30, 90°, 150°
જવાબ
(D) 30, 90°, 150°
S1 અને S2 ના લીધે વર્તુળના પરિધ પરના જે બિંદુઓએ સહાયક વ્યતિકરણ રચાય તે શોધવાના છે.
∴ S1 અને S2 ના સહાયક વ્યતિકરણ માટે પથ-તફાવત.
dsinθ = nλ જ્યાં n = 0, 1, 2, 3, 4 …
∴ 2λ sinθ = nλ
∴ sinθ =
sinθ નું મૂલ્ય 0° થી 180° સુધી જ ધન મળે તેથી અર્ધવર્તુળ પરના સહાયક વ્યતિકરણ રચાતા બિંદુઓ માટે ખૂણાઓ શોધવાના છે.
જો n = 0 ⇒ sinθ = 0
∴ θ = 0° અને 180°
જો n = 2 ⇒ sinθ = 1
∴ θ = 90°
જો n = 1 ⇒ sinθ =
∴ θ = 30° અને 150°
માટે અર્ધવર્તુળના પરિધ પરના વિકલ્પમાં આપેલાં બિંદુઓ (B)માં છે.
∴ θ = 30°, 90°, 150°
પ્રશ્ન 57.
મધ્યસ્થ પ્રકાશિત શલાકાની તીવ્રતા અને મધ્યબિંદુથી બે ક્રમિક શલાકાઓ
વચ્ચેનાં અંતરના ચોથા ભાગને અંતરે મળતી શલાકાની તીવ્રતાનો ગુણોત્તર શોધો.
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 16 : 1
જવાબ
(A) 2 : 1
મધ્યસ્થ અધિકતમની તીવ્રતા I0 ધારો.
બે ક્રમિક શલાકાઓ વચ્ચેનો કળા-તફાવત

પ્રશ્ન 58.
બે સુસમ્બદ્ધ ઉદ્ગમોમાંથી સરખી તરંગલંબાઈ અને સમાન કંપવિસ્તારવાળા પ્રકાશથી પડદાને પ્રકાશિત કરેલો છે. મધ્યસ્થ અધિકતમની તીવ્રતા I0 છે. જો ઉદ્ગમો અસુસમ્બદ્ધ હોય તો તે જ બિંદુ પાસે પ્રકાશની તીવ્રતા કેટલી હોય ?
(A) 4I0
(B) 2I0
(C) I0
(D)
જવાબ
(D)
સુસમ્બદ્ધ ઉદ્ગમો હોય ત્યારે,
I0 = I1 + I2 + 2
∴ I0 = I + I + 2I [∵ કંપવિસ્તાર સમાન છે.]
∴ I0 = 4I …………….. (1)
હવે સુસમ્બદ્ધ ઉદ્ગમો હોય તો
IR = I1 + I2
= I + I
IR = 2I ……………. (2)
∴
IR =
પ્રશ્ન 59.
બે લિટના રંગના પ્રયોગમાં ……………………. વિભાજનથી સુસંબદ્ધ ઉદ્ગમો મેળવવામાં આવે છે.
(A) કંપવિસ્તાર
(B) તરંગલંબાઈના
(C) તરંગઅગ્રના
(D) આવૃત્તિના
જવાબ
(C) તરંગઅગ્રના
પ્રશ્ન 60.
રંગના પ્રયોગમાં બે ક્રમિક પ્રકાશિત અથવા ક્રમિક અપ્રકાશિત શલાકાઓ વચ્ચેનું અંતરનું સૂત્ર ………………….
(A)
(B)
(C)
(D)
જવાબ
(C)
પ્રશ્ન 61.
રંગના પ્રયોગમાં ઉદ્ગમથી પડદા વચ્ચેનું અંતર વધારીએ તો, શલાકાઓની પહોળાઈ ………………………..
(A) અચળ રહે છે.
(B) વધે છે.
(C) ઘટે છે.
(D) કંઈ કહી શકાય નહીં.
જવાબ
(B) વધે છે.
∴
પ્રશ્ન 62.
રંગના પ્રયોગમાં બે સુસંબદ્ધ ઉદ્ગમો વચ્ચેનું અંતર d વધારતાં શલાકાની પહોળાઈ ………………….
(A) વધે છે.
(B) ઘટે છે.
(C) અચળ રહે છે.
(D) કંઈ કહી શકાય નહીં.
જવાબ
(B) ઘટે છે.
∴
∴
પણ d વધારતાં
પ્રશ્ન 63.
ચંગના પ્રયોગમાં વપરાયેલ પ્રકાશની તરંગલંબાઈ વધારતાં બે ક્રમિક શલાકા વચ્ચેનું અંતર …………………….
(A) વધે
(B) ઘટે
(C) અચળ રહે
(D) કાંઈ કહી શકાય નહીં
જવાબ
(A) વધે
∴
∴
∴ λ વધે તો
પ્રશ્ન 64.
રંગના પ્રયોગમાં પડદા પર શલાકાની પહોળાઈ 0.2 mm જેટલી છે. જો વ્યતિકરણ
ઊપજાવતા પ્રકાશની તરંગલંબાઈમાં 10 % નો વધારો કરવામાં આવે તથા S1 અને S2 બે સ્લિટો વચ્ચે અંતર પણ 10 % વધારવામાં આવે, તો નવી શલાકાઓની પહોળાઈ ……………………… mm થશે.
(A) 0.20
(B) 0.401
(C) 0.242
(D) 0.165
જવાબ
(A) 0.20
શલાકાની પહોળાઈ β =
β ∝
∴
∴
∴ β2 = β1 ∴ β2 = 0.2 mm
પ્રશ્ન 65.
રંગના એક પ્રયોગમાં બે લિટ વચ્ચેનું અંતર 0.2 mm છે. જો પ્રયોગમાં વપરાયેલ
પ્રકાશની તરંગલંબાઈ 5000 A હોય, તો ત્રીજી પ્રકાશિત શલાકાનું મધ્યસ્થ
શલાકાથી કોણીય અંતર ……………………… rad હશે.
(A) 0.75
(B) 0.075
(C) 0.0075
(D) 0.057
જવાબ
(C) 0.0075
‘n’ મી પ્રકાશિત શલાકા માટે
dsinθ = nλ માં,
n = 3, d = 0.02 cm, λ = 5 × 10-5 cm
∴ sinθ =
∴ sinθ =
∴ sinθ = 0.0075 rad
પ્રશ્ન 66.
યંગના ડબલ લિટના પ્રયોગમાં એકરંગી ઉદ્ગમનો ઉપયોગ કરતાં પડદા પર મળતી વ્યતિકરણ શલાકાનો આકાર ………………………
(A) પરવલય
(B) વર્તુળ
(C) સુરેખ
(D) અતિવલય
જવાબ
(D) અતિવલય
પ્રશ્ન 67.
એક બિંદુએ સંપાત થતા સમાન તરંગલંબાઈવાળા બે તરંગો વચ્ચે પથ તફાવત 130 જેટલો
છે, તો તે બિંદુએ …………………….. પ્રકારનું અને …………………….. ક્રમનું વ્યતિકરણ
રચાશે.
(A) સહાયક, 13મા
(B) વિનાશક, 13મા
(C) સહાયક, 7મા
(D) વિનાશક, 7મા
જવાબ
(A) સહાયક, 13 મા
 =
=
∴ આ બિંદુએ સહાયક પ્રકારનું અને 13 મા ક્રમનું વ્યતિકરણ રચાશે.
પ્રશ્ન 68.
યંગના પ્રયોગમાં પડદા પર આવેલા P બિંદુ આગળ 5 મા ક્રમની અપ્રકાશિત શલાકા રચાય છે, તો ઉદ્ગમસ્થાનથી P બિંદુ આગળનો પથ તફાવત ……………………….
(A)
(B)
(C)
(D)
જવાબ
(C)
અપ્રકાશિત શલાકા માટે,
પથ તફાવત = (2n – 1)
પ્રશ્ન 69.
યંગના પ્રયોગમાં 5મી અપ્રકાશિત અને 3જી પ્રકાશિત શલાકા વચ્ચેનું અંતર x5 – x3 = ……………………. β.
(A) 2
(B) 3
(C)
(D)
જવાબ
(D)
5મી અપ્રકાશિત શલાકા માટે,
x5 =
3જી પ્રકાશિત શલાકા માટે
x3 =
x5 – x3 =
=
પ્રશ્ન 70.
યંગના પ્રયોગમાં પડદાના જે ભાગમાં મધ્યમાનથી ત્રીજી અપ્રકાશિત શલાકા મળે છે ત્યાં બે તરંગોની કળાનો તફાવત ……………………. હોય છે.
(A) 3π
(B) 4π
(C) શૂન્ય
(D) 5π
જવાબ
(D) 5π
અપ્રકાશિત શલાકામાં કળા તફાવત = (2n – 1)π = 5π
પ્રશ્ન 71.
એક બિંદુએ સંપાત થતા સમાન તરંગલંબાઈવાળા બે તરંગો વચ્ચે પથતફાવત
(A) વિનાશક, બીજા
(B) સહાયક, બીજા
(C) વિનાશક, ત્રીજા
(D) સહાયક, ચોથા
જવાબ
(A) વિનાશક, બીજા
પથ તફાવત =
પ્રશ્ન 72.
યંગના પ્રયોગમાં બે ક્રમિક અપ્રકાશિત શલાકા વચ્ચેનું અંતર 2 mm છે, તો મધ્યમાનથી ત્રીજી અપ્રકાશિત શલાકાનું અંતર ……………………. છે.
(A) 3 mm
(B) 1.5 mm
(C) 2.5 mm
(D) 5 mm
જવાબ
(D) 5 mm
xn = (2n – 1)
=
પ્રશ્ન 73.
યંગના ડબલ સ્લિટના પ્રયોગમાં સોડિયમ પ્રકાશને બદલે સફેદ પ્રકાશનો ઉપયોગ કરવામાં આવે તો …………………………..
(A) બધી શલાકાઓ અપ્રકાશિત દેખાશે.
(B) બધી પ્રકાશિત શલાકાઓ સફેદ દેખાશે.
(C) ફક્ત મધ્યસ્થ શલાકા સફેદ હશે, બાકીની બધી રંગીન દેખાશે.
(D) એક પણ નહીં.
જવાબ
(C) ફક્ત મધ્યસ્થ શલાકા સફેદ હશે. બાકીની બધી રંગીન દેખાશે.
β =
પ્રશ્ન 74.
યંગના પ્રયોગમાં 5890.Å તરંગલંબાઈવાળો પીળો પ્રકાશ વાપરવામાં આવે તો
શલાકાની કોણીય પહોળાઈ 0.2° માલૂમ પડે છે. કોણીય પહોળાઈ 10 % વધારવા તેની
તરંગલંબાઈમાં કેટલો ફેરફાર કરવો પડે ?
(A) તરંગલંબાઈમાં 589 Å જેટલો વધારો કરવો પડે.
(B) તરંગલંબાઈમાં 589 Å જેટલો ઘટાડો કરવો પડે.
(C) તરંગલંબાઈમાં 6479 Å જેટલો વધારો કરવો પડે.
(D) તરંગલંબાઈમાં કોઈ જ ફેરફાર ન કરવો પડે.
જવાબ
(A) તરંગલંબાઈમાં 589 Å જેટલો વધારો કરવો પડે.
શલાકાની કોણીય પહોળાઈ 2(dsinθ) = 2(1)λ
∴ 2θ =
આ સૂત્રમાં જો d અચળ હોય તો θ ∝ λ
∴
θ2 = θ1 + 10 % θ1
= 1.1θ1
∴
∴ 
∴ λ2 = 5890 Å × 1.1
∴ λ2 = 6479 Å
∴ તરંગલંબાઈમાં વધારો = λ2 – λ1
= 6479 – 5890
= 589 Å
પ્રશ્ન 75.
રંગના બે લિટના પ્રયોગમાં એક લિટથી નીકળતા તરંગના એક કિરણના માર્ગમાં t
જાડાઇની અને μ વક્રીભવનાંકવાળી માઇકાની તકતી મૂકતાં પડદા પર મળતી શલાકાઓ
………………… અંતર ખસશે.
(A)
(B)
(C)
(D)
જવાબ
(B)
યંગના પ્રયોગમાં એક સ્વિટમાંથી નીકળતા કિરણના માર્ગમાં t જાડાઈની μ વક્રીભવનાંકવાળી તકતી મૂકતાં પથ-તફાવત = (μ – 1)t થાય.
પણ આ પથ-તફાવત =
∴ (μ – 1)t =
∴ x =
∴ શલાકા
પ્રશ્ન 76.
રંગના પ્રયોગમાં બે લિટમાંથી આવતાં કિરણો પૈકી એક કિરણના માર્ગમાં d
જાડાઈની અને n વક્રીભવનાંકવાળી કાચની પ્લેટ મૂકવામાં આવે ત્યારે જો મધ્યસ્થ
પ્રકાશિત શલાકાની તીવ્રતા શૂન્ય મળે તો તે માટે આ પ્લેટની લઘુતમ જાડાઈ
…………………. હોવી જોઈએ. પ્રકાશની તરંગલંબાઈ λ છે.
(A) (n – 1)
(B)
(C)
(D) (n – 1) λ
જવાબ
(C)
યંગના પ્રયોગમાં એક સ્વિટમાંથી નીકળતા કિરણના માર્ગમાં જાડાઈની ‘n’ વક્રીભવનાંકવાળી કાચની પ્લેટ મૂકતાં પથ-તફાવત (n – 1)d થાય.
પ્રકાશની તીવ્રતા શૂન્ય મળે તો અપ્રકાશિત હોય
∴ ‘m’ મા ક્રમની અપ્રકાશિત શલાકા માટે,
પથ-તફાવત (2m – 1)
∴ (n – 1)d = (2m – 1)
પ્લેટની લઘુતમ જાડાઈ માટે m = 1
∴ (n – 1)d =
∴ d =
પ્રશ્ન 77.
યંગના બે લિટના પ્રયોગને હવાના બદલે પાણીમાં કરવામાં આવે છે. પાણીને સ્થિર અને સ્વચ્છ ધારીને કહી શકાય કે શલાકાની ભાત ………………………
(A) બદલાશે નહીં
(B) અદશ્ય થશે
(C) સંકોચાશે
(D) વિવર્ધિત થશે.
જવાબ
(C) સંકોચાશે
પ્રશ્ન 78.
S1 અને S2 ઉદ્ગમોમાંથી ઉદ્ભવતાં બે તરંગોની કળાનો
તફાવત શૂન્ય અને λ જેટલી સમાન તરંગલંબાઈ છે. આ તરંગો P બિંદુ પાસે સંપૂર્ણ
વિનાશક વ્યતિકરણ રચે તો S1P – S2P = ……………………
(A) 5λ
(B)
(C)
(D)
જવાબ
(D)
વિનાશક વ્યતિકરણની શરત = (2n – 1)
જ્યાં, n = પૂર્ણાંક સંખ્યા
∴ (2n – 1) એ એકી સંખ્યા મળે.
શરત = એકી સંખ્યા ×
પ્રશ્ન 79.
રંગના એક પ્રયોગમાં બે લિટ વચ્ચેનું અંતર 0.4 cm અને સ્લિટથી પડદાનું અંતર
100 cm છે, પ્રયોગમાં વપરાયેલ પ્રકાશની તરંગલંબાઈ 5000 Å હોય તો, ચોથી
અપ્રકાશિત શલાકાનું મધ્યસ્થ શલાકાથી અંતર ……………………. હશે.
(A) 4.37 × 10-2 cm
(B) 4.37 mm
(C) 8.74 × 10-2 cm
(D) 8.74 mm
જવાબ
(A) 4.37 × 10-2 cm
‘n’ મી અપ્રકાશિત શલાકા માટે,
d sinθn = (2n – 1)
પણ sinθn =
∴ xn =
λ = 5 × 10-5cm, D = 100 cm અને n = 4
∴ x4 =
=
∴ x4 = 4.37 × 10-2 cm
પ્રશ્ન 80.
સોડિયમ પ્રકાશ (λ = 5898 Å) નો ઉપયોગ કરી યંગનો બે લિટનો પ્રયોગ દર્શાવતા
પડદા પરના ચોક્કસ અંતર R માં 92 શલાકા મળે છે. જો આપેલા રંગના (λ = 5481 Å)
નો ઉપયોગ કરવામાં આવે તો તેટલા અંતરમાં કેટલી શલાકાઓ મળે ?
(A) 62
(B) 67
(C) 85
(D) 99
જવાબ
(D) 99
અહીં, λ1 = 5898 Å, λ2 = 5481 Å, n1 = 92 છે.
હવે R = n1
∴
∴
∴
∴ n2 = n1 ×
∴ n2 = 99
પ્રશ્ન 81.
રંગના પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર અડધું કરવામાં આવે અને સ્લિટ તથા
પડદા વચ્ચેનું અંતર બમણું કરવામાં આવે તો શલાકાની પહોળાઈ …………………… (NEET –
2020)
(A) બદલાતી નથી.
(B) અડધી થાય છે.
(C) બમણી થાય છે.
(D) ચાર ગણી થાય છે.
જવાબ
(D) ચાર ગણી થાય છે.

પ્રશ્ન 82.
રંગના પ્રયોગમાં એક કિરણના માર્ગમાં λ જાડાઈની અને 1.5 વક્રીભવનાંક ધરાવતી
પ્લેટ મૂકવામાં આવે છે. હવે જો મધ્યસ્થ શલાકા પ્રકાશિત રહેતી હોય તો
પ્લેટની લઘુતમ જાડાઈ ……………………… હોય. [IIT – 2002]
(A) 2λ
(B) λ
(C)
(D)
જવાબ
(A) 2λ
પ્લેટની જાડાઈ = d =
અહીં, m = 1 અને n = 1.5 લેતાં,
d =
∴ d = 2λ
પ્રશ્ન 83.
ચંગના પ્રયોગમાં જો એક લિટ, બીજી સ્લિટ કરતાં બમણી પહોળાઈની લેવામાં આવે, તો વ્યતિકરણમાં ……………………..
(A) પ્રકાશિત અને અપ્રકાશિત શલાકાઓની તીવ્રતા વધશે.
(B) પ્રકાશિત શલાકાઓની તીવ્રતા વધશે અને અપ્રકાશિત શલાકાઓની તીવ્રતા શૂન્ય થશે.
(C) પ્રકાશિત શલાકાઓની તીવ્રતા ઘટશે અને અપ્રકાશિત શલાકાઓની તીવ્રતા વધશે.
(D) પ્રકાશિત શલાકાઓની તીવ્રતા ઘટશે અને અપ્રકાશિત શલાકાઓની તીવ્રતા શૂન્ય થશે.
જવાબ
(A) પ્રકાશિત અને અપ્રકાશિત શલાકાઓની તીવ્રતા વધશે.
સ્વિટની પહોળાઈના સમપ્રમાણમાં પ્રકાશની તીવ્રતા મળે અને તીવ્રતા ∝ (કંપવિસ્તાર)2
∴ જુદા જુદા કંપવિસ્તાર ધારો કે E1 અને E2 વાળા તરંગોના સંપાતીકરણ થતાં સહાયક વ્યતિકરણ રચાતા બિંદુએ પ્રકાશની તીવ્રતા
Imax = (E1 + E2)2 એટલે વધે
અને વિનાશક વ્યતિકરણ રચાતા બિંદુએ પ્રકાશની તીવ્રતા
Imin = (E2 – E1)2 જો E1 < E2
= (2E1 – E1)2
= E12
એટલે શલાકાની તીવ્રતા વધે.
પ્રશ્ન 84.
કંગના વ્યતિકરણના પ્રયોગમાં 640 nm તરંગલંબાઈનો પ્રકાશ વાપરતા શલાકાની પહોળાઈ 2.4 × 10-4m મળે છે. શલાકાની પહોળાઈમાં 0.9 × 10-4 m નો ઘટાડો મેળવવા તરંગલંબાઈવાળો પ્રકાશ વાપરવો જોઈએ.
(A) 640 nm
(B) 465 nm
(C) 880 nm
(D) 550 nm
જવાબ
(B) 465 nm

∴ λ2 = 640 ×
∴ λ2 = 465 nm ∴ λ2 ≈ 465.4 nm
પ્રશ્ન 85.
રંગના બે સ્વિટના પ્રયોગમાં વ્યતિકરણ રચતા તરંગોમાંના એક તરંગના પથમાં 1.5
વક્રીભવનાંક ધરાવતી ગ્લાસની પ્લેટ મૂકતાં શલાકાભાત y અંતર ખસે છે. જ્યારે આ
પ્લેટની જગ્યાએ બીજી તેટલી જ જાડાઈની માઈકાની શીટ મૂકતા શલાકાની ભાત
(A) 1.50
(B) 1.75
(C) 1.25
(D) 1.00
જવાબ
(B) 1.75
યંગના પ્રયોગમાં t જાડાઈ અને n વક્રીભવનાંકવાળી પ્લેટને એક કિરણના માર્ગમાં મૂકતાં પથ-તફાવત = (n – 1)t અને
શલાકાની શિફ્ટ x =
∴ કાચની પ્લેટ મૂકતાં y =
અને માઈકાની પ્લેટ મૂકતાં
બંનેનો ગુણોત્તર લેતાં,
∴ 2n2 – 2 = – 3n1 – 3
∴ 2n2 = 3 × 1.5 – 3 + 2
∴ 2n2 = 4.5 – 1
∴ 2n2 = 3.5
∴ n2 = 1.75
પ્રશ્ન 86.
યંગના એક પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર 0.055 cm અને સ્લિટથી પડદાનું
અંતર 100 cm છે. તો મધ્યબિંદુથી ઉપર તરફ બીજી પ્રકાશિત અને મધ્યબિંદુથી
નીચે તરફ ચૌથી અપ્રકાશિત શલાકા વચ્ચેનું અંતર શોધો. પ્રકાશની તરંગલંબાઈ
4000 Å છે.
(A) 0.3 cm
(B) 0.5 cm
(C) 0.4 cm
(D) 0.6 cm
જવાબ
(C) 0.4 cm
મધ્યસ્થ અધિકતમની એક બાજુએ બીજી પ્રકાશિત શલાકાનું અંતર
x2 =
∴ x2 =
અને મધ્યસ્થ અધિકતમની બીજી બાજુએ રહેલ ચોથી અપ્રકાશિત
શલાકાનું અંતર,
x’n (2n – 1)
∴ x’3
∴ બીજી પ્રકાશિત અને ચોથી અપ્રકાશિત શલાકા વચ્ચેનું અંતર
x2 + x’3 =
x2 + x’3 =
=
= 4 × 10-5 × 104 = 0.4 cm
પ્રશ્ન 87.
યંગના બે લિટનો પ્રયોગ પ્રવાહીમાં કરતાં પ્રવાહીમાં 10 મી પ્રકાશિત શલાકા
અને હવામાં છઠ્ઠી અપ્રકાશિત શલાકા હવામાં મળે છે. તો પ્રવાહીનો વક્રીભવનાંક
આશરે ………………… .
(A) 1.2
(B) 1.6
(C) 1.5
(D) 1.8
જવાબ
(D) 1.8
જ્યારે પ્રયોગના સાધનો પ્રવાહીમાં ડુબાડેલા હોય તો તરંગલંબાઈ
10મી પ્રકાશિત શલાકા પ્રવાહીમાં મળે છે.
∴ x =
છઠ્ઠી અપ્રકાશિત શલાકા હવામાં મળે છે.
∴ x = (2 × 6 – 1)
સમી. (1) અને (2) સમાન
∴ n = 1.818 ∴ n ≈ 1.8
પ્રશ્ન 88.
યંગના ડબલ સ્લિટના પ્રયોગમાં S1 અને S2 લિટમાંથી નીકળતા કિરણોથી xy પડદા પર મળતી વ્યતિકરણ શલાકા આકૃતિમાં દર્શાવ્યા પ્રમાણે મળે છે. તો શલાકા ખરેખર કેવી દેખાશે ?

(A) PQ
(B) W1W2
(C) W3W4
(D) xy
જવાબ
(C) W3W4
સ્વિટની લંબાઈને સમાંતર પડદા xy પર વ્યતિકરણ શલાકા વક્ર દેખાશે.
પ્રશ્ન 89.
યંગના પ્રયોગમાં સ્લિટની સામે t જાડાઈની પાતળી પારદર્શક તકતી મૂકવામાં આવે, તો શલાકાની પહોળાઈ …………………..
(A) વધે
(B) ઘટે
(C) t ગણી થાય
(D) બદલાતી નથી
જવાબ
(D) બદલાતી નથી
પ્રશ્ન 90.
યંગના પ્રયોગમાં જ્યારે બંને સ્લિટો કાર્યરત હોય, ત્યારે મધ્યસ્થ પ્રકાશિત
શલાકાના સ્થાને તીવ્રતા I મળે છે. જો બે પૈકી એક સ્વિટને ઢાંકી દેવામાં
આવે, તો તે સ્થાને પ્રકાશની તીવ્રતા …………………….. (આ સ્થાને વ્યતિકરણ રચાશે
નહીં)
(A) 0
(B) \(\frac{\mathrm{I}}{2}[latex]
(C) I
(D) [latex]\frac{\mathrm{I}}{4}[latex]
જવાબ
(D) [latex]\frac{\mathrm{I}}{4}[latex]
પ્રારંભમાં I ∝ (E + E)2 ⇒ I = (2E)2
∴ I ∝4E2 ………… (1)
હવે એક સ્લિટ બંધ કરતાં I’ = (E + 0)2
∴ I’ = E2 ……………… (2)
∴ સમીકરણ (2) અને (1)નો ગુણોત્તર લેતાં,
[latex]\frac{\mathrm{I}^{\prime}}{\mathrm{I}}=\frac{\mathrm{E}^2}{4 \mathrm{E}^2}\) I’ = \(\frac{\mathrm{I}}{4}[latex]
પ્રશ્ન 91.
યંગના પ્રયોગમાં ગોઠવણી અફર રાખી માત્ર પીળા પ્રકાશના સ્થાને લાલ પ્રકાશના ઉદ્ગમનો ઉપયોગ કરવામાં આવે, તો …………………..
(A) શલાકાઓની તીવ્રતા ઘટે.
(B) શલાકાઓની પહોળાઈ ઘટે.
(C) શલાકાઓની પહોળાઈ વધે.
(D) બે ક્રમિક શલાકાઓ વચ્ચેનું અંતર અચળ રહે.
જવાબ
(C) શલાકાઓની પહોળાઈ વધે.
શલાકાની પહોળાઈ β ∝ λ અને λy < λR
પ્રશ્ન 92.
રંગના પ્રયોગમાં λ1 તરંગલંબાઈથી 8મી પ્રકાશિત શલાકા, λ2 તરંગલંબાઈથી 9મી પ્રકાશિત શલાકાના સ્થાને મળે છે, તો = λ1 …………………. અને λ2 = ……………..
(A) 450 nm, 400 nm
(B) 400 nm, 450 nm
(C) 450 nm, 450 nm
(D) 400 nm, 400 nm
જવાબ
(A) 450 nm, 400 nm
અહીં θ8 = θ9
∴ dsinθ8 = dsinθ9
∴ n1λ1 = n2λ2
∴ 8λ1 = 9λ2
∴ [latex]\frac{8}{9}=\frac{\lambda_2}{\lambda_1}\)
∴
∴ λ1 = 4 × 100 = mm = 400 mm,
λ1 = 4.5 × 100 = 450 mm
પ્રશ્ન 93.
યંગના પ્રયોગમાં શલાકાની પહોળાઈ β મળે છે. જો પ્રયોગની ગોઠવણ અફર રાખીને n
વક્રીભવનાંકવાળા પ્રવાહીમાં આ પ્રયોગ કરવામાં આવે, તો શલાકાની પહોળાઈ
………………..
(A)
(B) nβ
(C)
(D)
જવાબ
(C)
હવામાં શલાકાની પહોળાઈ β =
અને પ્રવાહીમાં તરંગલંબાઈ λ’ =
∴ પ્રવાહીમાં શલાકાની પહોળાઈ β’ =
∴ β’ =
પ્રશ્ન 94.
સ્વિટમાંથી પસાર થતી વખતે તરંગોના સ્વિટની ઘાર આગળથી વાંકા વળવાની ઘટનાને ……………………. કહે છે.
(A) પરાવર્તન
(B) વક્રીભવન
(C) વિવર્તન
(D) પ્રકીર્ણન
જવાબ
(C) વિવર્તન
પ્રશ્ન 95.
વિવર્તનની ઘટનાની શોધ ………………….. નામના વૈજ્ઞાનિકે કરી હતી.
(A) યંગ
(B) હાઇગેન્સ
(C) ફ્રોનહૉફર
(D) ગ્રિમાલ્ડી
જવાબ
(D) ગ્રિમાલ્ડી
પ્રશ્ન 96.
વિવર્તનનો મુખ્ય આધાર …………………. ગુણોત્તર પર છે.
(A)
(B)
(C)
(D)
જ્યાં λ = તરંગલંબાઈ, D = સ્લિટથી પડદાનું અંતર, a = સ્વિટની પહોળઈ.
જવાબ
(C)
પ્રશ્ન 97.
જો
(A) વધે છે
(B) ઘટે છે
(C) બદલાતી નથી
(D) શૂન્ય
જવાબ
(A) વધે છે
પ્રશ્ન 98.
મહત્તમ વિવર્તન માટેની શરત …………………..
(A)
(B)
(C)
(D)
જવાબ
(A)
પ્રશ્ન 99.
……………………. ની ઘટના કિરણ પ્રકાશશાસ્ત્રની મદદથી સમજાવી શકાય નહીં.
(A) પરાવર્તન
(B) વક્રીભવન
(C) વિવર્તન
(D) પૂર્ણ આંતરિક પરાવર્તન
જવાબ
(C) વિવર્તન
પ્રશ્ન 100.
વિવર્તન એટલે ……………………..
(A) તરંગ-અગ્રનું વળાંક લેવું.
(B) અંતરાયથી નહિ રોકાયેલા મર્યાદિત તરંગ-અગ્ર વડે નિપજાતી અસર.
(C) તરંગ-અગ્રનો વેગઘટાડો.
(D) તરંગ-અગ્રનું વિભાજન.
જવાબ
(B) અંતરાયથી નહિ રોકાયેલા મર્યાદિત તરંગ-અગ્ર વડે નિપજાતી અસર.
પ્રશ્ન 101.
લાલ રંગ વડે મળતી વિવર્તન ભાતને બદલે જાંબલી રંગ વડે વિવર્તન ભાત મેળવવામાં આવે તો ……………………..
(A) વિવર્તન ભાત અદૃશ્ય થશે.
(B) વિવર્તન ભાત છૂટી-છૂટી દેખાશે.
(C) વિવર્તન ભાત અચળ રહેશે.
(D) વિવર્તન ભાત સાંકડી બનશે.
જવાબ
(D) વિવર્તન ભાત સાંકડી બનશે.
વિવર્તન sinθ =
∴ sinθ ∝ λ અને λV < λR
∴ sinθV < sinθR
પ્રથમ ચરણમાં sin વિધેય વધતું વિધેય છે.
∴ θV < θR
∴ જાંબલી રંગથી મળતી વ્યતિકરણ શલાકાની ભાત નજીક નજીક (સાંકડી) મળે.
પ્રશ્ન 102.
શ્વેત પ્રકાશ માટે એક સ્લિટ વડે રચાતા વિવર્તનની મધ્યસ્થ શલાકા ……………………. રંગની હશે.
(A) કાળા
(B) વાદળી
(C) લાલ
(D) સફેદ
જવાબ
(D) સફેદ
પ્રશ્ન 103.
એક સ્વિટના વિવર્તનના પ્રયોગમાં મળતી મધ્યસ્થ અધિકતમનું કોણીય અંતર ………………………. વધારી શકાય છે.
(A) તરંગલંબાઈ ઘટાડીને
(B) સ્લિટ અને પડદા વચ્ચેનું અંતર વધારીને
(C) સ્વિટની પહોળાઈ વધારીને
(D) સ્વિટની પહોળાઈ ઘટાડીને
જવાબ
(D) સ્વિટની પહોળાઈ ઘટાડીને
એક સ્વિટના વિવર્તનથી મળતી મધ્યસ્થ અધિકતમ માટેની શરત,
d sinθ = λ ⇒ sinθ =
∴ sinθ ∝ λ અને sinθ ∝
∴ λ વધારીને અથવા સ્વિટની પહોળાઈ a ઘટાડીને sinθ વધારી શકાય અને sin વિધેય વધતું હોવાથી a ઘટાડીને θ (કોણીય અંતર) વધારી શકાય.
પ્રશ્ન 104.
એક લિટથી થતાં વિવર્તનમાં ‘n’ ક્રમનાં ન્યૂનતમ માટેની શરત ……………….. જ્યાં n = ± 1, ± 2, ± 3, …………….
(A) nλ = asinθn
(B) aλ = nsinθn
(C)
(D) nλ =
જવાબ
(A) nλ = asinθn
પ્રશ્ન 105.
એક લિટથી રચાતા વિવર્તન માટે ‘n’ ક્રમના અધિકતમ માટેની શરત …………………… જ્યાં n = 1, 2, 3, …
(A) asinθ’n = (n –
(B) asinθ’n = (n +
(C) λasinθ’n = (n –
(D) λsinθ’n = (n +
જવાબ
(B) asinθ’n = (n +
પ્રશ્ન 106.
ફ્રોનહૉફર વિવર્તનમાં જેમ શલાકાનો ક્રમ વધતો જાય તેમ …………………….
(A) શલાકાની પહોળાઈ અને તીવ્રતા વધતી જાય.
(B) શલાકાની પહોળાઈ અને તીવ્રતા ઘટતી જાય.
(C) શલાકાની પહોળાઈ અને તીવ્રતા ન બદલાય.
(D) શલાકાની પહોળાઈ ઘટે પણ તીવ્રતા વધતી જાય.
જવાબ
(B) શલાકાની પહોળાઈ અને તીવ્રતા ઘટતી જાય.
પ્રશ્ન 107.
વિવર્તન માટે મધ્યસ્થ અધિકતમની કોણીય પહોળાઈ અને રેખીય પહોળાઈનું સૂત્ર ……………………… છે.
(A) β = 2β0
(B) β =
(C) β = β0
(D) શક્ય નથી
જવાબ
(B) β =
જ્યાં β = રેખીય પહોળાઈ અને β0 = કોણીય પહોળાઈ છે.
પ્રશ્ન 108.
ફ્રોનહોફર વિવર્તનમાં આપાતપ્રકાશની તરંગલંબાઈ 4000 Å છે. પ્રથમ ન્યૂનતમ 30° ના કોણે મળે છે, તો મધ્યસ્થ અધિકતમનો કોણ ……………………….
(A) sin-1(
(B) sin-1(
(C) sin-1(
(D) tan -1(
જવાબ
(B) sin-1(
‘m’માં ક્રમના અધિકતમ માટે,
asinθ’ = (2m + 1)
∴ asinθ’ =
‘m’માં ક્રમના ન્યૂનતમ માટે,
asinθ = λ
asin30° = λ
a ×
a = 2λ
∴ પરિણામ (1) પરથી,
2λ × sinθ’ =
sinθ’ =
∴ θ = sin-1(
પ્રશ્ન 109.
ફ્રોનહોફર વિવર્તનનો પ્રથમ ન્યૂનતમ માટેનો વિવર્તનકોણ
(A) λ
(B) 2λ
(C)
(D)
જવાબ
(B) 2λ
d sinθ = nλ માં n = 1, θ =
∴ d =
∴ d = 2λ
પ્રશ્ન 110.
નીચેનામાંથી કોનું વિવર્તન વધુમાં વધુ હશે ?
(A) γ કિરણો
(B) રેડિયો તરંગો
(C) અલ્ટ્રાવાયોલેટ તરંગો
(D) ઇન્ફ્રારેડ તરંગો
જવાબ
(B) રેડિયો તરંગો
વિવર્તનનો આધાર λ પર છે. જેમ નું મૂલ્ય મોટું તેમ વિવર્તન વધારે અને આપેલાં તરંગો પૈકી રેડિયો તરંગોની તરંગલંબાઈ સૌથી વધુ છે.
પ્રશ્ન 111.
આપેલ સ્લિટ માટે પ્રથમ મહત્તમ અને પ્રથમ ન્યૂનતમ શલાકાઓના વિવર્તનકોણનો ગુણોત્તર ……………………….. છે.
(A)
(B)
(C)
(D)
જવાબ
(D)
m મા અધિકતમ માટેની શરત,
asinθm = (2m + 1)
sinθ1 =
‘m’ મા ન્યૂનતમ માટેની શરત,
sinθ’m =
∴
પ્રશ્ન 112.
55 nm તરંગલંબાઈવાળા પ્રકાશ દ્વારા 0.55 mm પહોળાઈની સ્લિટ દ્વારા મળતા વિવર્તનમાં પ્રથમ ક્રમના મહત્તમનો વિવર્તન કોણ કેટલો ?
(A) 0.0015 રેડિયન
(B) 0.00015 રેડિયન
(C) 0.003 રેડિયન
(D) 0.0010 રેડિયન
જવાબ
(B) 0,00015 રેડિયન
પ્રથમ અધિકતમ માટે, asinθm =
asinθ1 =
λ = 5 × 10-7m
a = 55 × 10-5m
∴ sinθ1 =
પ્રશ્ન 113.
ધ્વનિના એક તરંગની આવૃતિ 600Hz છે. આ તરંગ 0.75m પહોળાઈના ખુલ્લા બારણા પર લંબરૂપે આપાત થાય છે. તો ક્યા કોણે પ્રથમ ન્યૂનતમ મળશે ?
(ધ્વનિની હવામાં ઝડપ 330 m/s છે)
(A) 20.8
(B) 45°
(C) 47.2°
(D) 83.6°
જવાબ
(C) 47.2°
m મા ક્રમના ન્યૂનતમ માટે d sinθm = mλ
0.75 sin1 = λ ……….. (1)
પણ v = λf ⇒ λ =
∴ 0.75 sin1 =
∴ sinθ1 =
∴ sinθ1 = 0.7333 ∴ θ1 = 47° 10′ 47.2°
પ્રશ્ન 114.
એકરંગી પ્રકાશનું સમતલ તરંગ-અગ્ર એક સ્લિટ પર લંબરૂપે આપાત થાય છે તેથી
પડદા પર વિવર્તન ભાત રચાય છે, જ્યાં પ્રથમ ન્યૂનતમ રચાય છે ત્યાં લિટની
ઉપરની ધાર અને નીચેની ધારમાંથી નીકળતાં તરંગો વચ્ચેનો કળા-તફાવત કેટલો હશે ?
(A) 0 rad
(B)
(C) π rad
(D) 2π rad
જવાબ
(D) 2π rad
સ્વિટની ઉપરની અને નીચેની ધારમાંથી નીકળતા તરંગો વચ્ચેનો કળા-તફાવત,
Φ =
પ્રથમ ન્યૂનતમ માટેની શરત
asinθ = λ
∴ Φ =
∴ Φ = 2π rad
પ્રશ્ન 115.
6980 Å વાળો પ્રકાશ સ્લિટ પર આપાત કરતાં 4° ના કોણે મધ્યસ્થ અધિકતમની બંને
બાજુએ પ્રથમ ન્યૂનતમ રચાતી હોય તો લિટની પહોળાઈ …………………… mm થશે.
(A) 0.2
(B) 2 × 10-5
(C) 2× 105
(D) 0.02
જવાબ
(D) 0.02
પ્રથમ ન્યૂનતમ માટે asinθ1 = nλ
a =
∴ a =
∴ a =
= 2 × 10-3 cm = 0.002 cm = 0.02 mm
પ્રશ્ન 116.
એક સ્લિટથી થતાં ફ્રોનહોફર વિવર્તનમાં સ્લિટની પહોળાઈ 0.60 mm છે. સ્લિટને
લંબરૂપે આપાતપ્રકાશની તરંગલંબાઈ 600 nm છે. સ્લિટથી પડદાનું અંતર 60 cm છે.
તો મધ્યસ્થ અધિકતમની પહોળાઈ શોધો.
(A) 1.2 mm
(B) 0.6 mm
(C) 2.4 mm
(D) 4.8 mm
જવાબ
(A) 1.2 mm
મધ્યસ્થ અધિકતમની પહોળાઈ એટલે પ્રથમ ક્રમના બે ન્યૂનતમો વચ્ચેનું અંતર
= પ્રથમક્રમના ન્યૂનતમ માટેની શરત
x1 =
∴ મધ્યસ્થ અધિકતમની પહોળાઈ
2x1 =
=
= 12 × 10-2 cm = 1.2 mm
પ્રશ્ન 117.
600 mm ની તરંગલંબાઈનો પ્રકાશ અડચણ પર આપાત થાય અને 15 m અંતર સુધી પ્રકાશનું વાંકા વળવાનું ઓછું હોય, તો અડચણનું રેખીય પરિમાણ શોધો.
(A) 3 mm
(B) 2 mm
(C) 4 mm
(D) 5 mm
જવાબ
(A) 3 mm
ફ્રેનલ અંતર એટલે જે અંતર સુધી પ્રકાશના વાંકા વળવાનું ખૂબ ઓછું હોય તેવું અંતર.
Zf =
a =
=
=
=
પ્રશ્ન 118.
એક લિટથી થતા ફ્રોનહોફર વિવર્તનમાં સ્લિટને લંબરૂપે આપાત પ્રકાશની
તરંગલંબાઈ બમણી કરવામાં આવે, સ્લિટથી પડદાનું અંતર ત્રણ ગણું કરવામાં આવે
અને
લિટની પહોળાઈ
(A) ત્રણ ગણી
(B) ચાર ગણી
(C) બમણી
(D) અડધી
જવાબ
(B) ચાર ગણી
વિવર્તનમાં મધ્યસ્થ અધિકતમની પહોળાઈ એટલે બે ન્યૂનતમો વચ્ચેનું અંતર
∴ મધ્યસ્થ અધિકતમની પહોળાઈ α =
∴ D અને a માં ફેરફાર કરવાથી મળતી નવી પહોળાઈ
α’ =
∴
∴ ચાર ગણી
પ્રશ્ન 119.
એક સ્વિટથી થતા ફ્રોનહોફર વિવર્તનમાં d પહોળાઈની સ્વિટને લંબરૂપે λ
તરંગલંબાઈવાળો પ્રકાશ આપાત કરવામાં આવે છે. સ્વિટથી પડદાનું અંતર D છે.
મધ્યસ્થ અધિકતમની રેખીય પહોળાઈ લિટની પહોળાઈથી અડધી હોય તો d = …………………….. .
(A)
(B)
(C)
(D)
જવાબ
(C)
મધ્યસ્થ અધિકતમની રેખીય પહોળાઈ એટલે પ્રથમક્રમના બે ન્યૂનતમ વચ્ચેનું રેખીય અંતર
પ્રથમક્રમના ન્યૂનતમ માટેની શરત
x1 =
∴ મધ્યસ્થ અધિકતમની રેખીય પહોળાઈ= x1 + x1
= 2x1
=
∴ a2 = 4λD
∴ a =
પ્રશ્ન 120.
વિવર્તનના પ્રયોગમાં સ્લિટની પહોળાઈ 0.6 nm છે. સ્લિટ પર પીળો પ્રકાશ આપાત
કરી વિવર્તન ભાત મેળવી શકાય છે. હવે પીળા પ્રકાશના સ્થાને X-rays નો ઉપયોગ
કરવામાં આવે તો ………………………. (MP-PMT-2002)
(A) વિવર્તનભાત મળશે નહીં.
(B) મધ્યસ્થ અધિકતમ પહોળું મળે.
(C) મધ્યસ્થ અધિકતમ સાંકડું મળે.
(D) શલાકાની સંખ્યા ઘટે.
જવાબ
(A) વિવર્તન ભાત મળશે નહીં.
વિવર્તનનો આધાર
પીળા પ્રકાશ માટે
∴ વિવર્તન શક્ય છે.

જે પીળા પ્રકાશ કરતાં ઘણો જ ઓછો હોવાથી વિવર્તન થશે નહિ તેથી વિવર્તન ભાત મળશે નહિ.
પ્રશ્ન 121.
ટેલિસ્કોપમાં વસ્તુકાચની કેન્દ્રલંબાઈ મોટી રાખવામાં આવે છે કારણ કે ………………………….
(A) લેન્સનો વ્યાસ મોટો બને, પરિણામે વિવર્તન ઓછું થાય.
(B) લેન્સનો વ્યાસ મોટો બને, પરિણામે વિવર્તન વધુ થાય.
(C) લેન્સનો વ્યાસ નાનો બને, પરિણામે વિવર્તન ઓછું થાય.
(D) આમાંથી એકપણ નહિ.
જવાબ
(A) લેન્સનો વ્યાસ મોટો બને, પરિણામે વિવર્તન ઓછું થાય.
પ્રશ્ન 122.
એક માઇક્રોસ્કોપની મદદથી એક બિંદુવત્ વસ્તુનું અવલોકન કરવામાં આવે છે. તેના
ઑબ્જેક્ટિવ વડે વસ્તુ પર આંતરાતો કોણ 20° છે. જો વસ્તુ અને ઑબ્જેક્ટિવ
વચ્ચે રાખેલ ઑઇલનો વક્રીભવનાંક 1.4 હોય તો ઑબ્જેક્ટિવનો …………………….. છે.
ન્યૂમેરિકલ એપરચર
(A) 0.24
(B) 0.48
(C) 2.4
(D) 4.8
જવાબ
(A) 0.24
ન્યૂમેરિકલ એપરેચર = nsinβ
= 1.4 sin(
= 1.4 sin 10° = 1.4 × 0.1736 = 0.24
પ્રશ્ન 123.
માઇક્રોસ્કોપના Oil Immersion ઑબ્જેક્ટિવ વડે વસ્તુ અંગેની બારીકાઇથી માહિતી મળી શકે છે. કારણ કે આવા ઑબ્જેક્ટિવ માટે ………………………
(A) વધારે મોટવણી હોય છે.
(B) વધારે વિભેદનશક્તિ હોય છે.
(C) વ્યાસ મોટો હોય છે.
(D) ઉપરનામાંથી એક પણ નહીં.
જવાબ
(B) વધારે વિભેદનશક્તિ હોય છે.
પ્રશ્ન 124.
10 cm વ્યાસવાળા ટેલિસ્કોપ માટે 5000 Å ના પ્રકાશ માટે કોણીય વિભેદન ………………….. ના ક્રમનું હોય.
(A) 106 rad
(B) 10-6 rad
(C) 10-4 rad
(D) 10-2 rad
જવાબ
(B) 10-6 rad
ટેલિસ્કોપનું કોણીય વિભેદન =
=
= 6.1 × 10-6 × 10-6 rad
પ્રશ્ન 125.
ટેલિસ્કોપમાં λ = 4000 Å અને λ = 6000 Å ના પ્રકાશ વડે મળતી વિભેદનશક્તિનો ગુણોત્તર …………………… છે.
(A) 4 : 5
(B) 3 : 2
(C) 2 : 3
(D) 5 : 4
જવાબ
(B) 3 : 2
ટેલિસ્કોપની વિભેદનશકિત =
∴ વિભેદનશક્તિ ∝
∴ ગુણોત્તર =
પ્રશ્ન 126.
એક ટેલિસ્કોપનો ઑબ્જેક્ટિવ લેન્સનો 5000 Å તરંગ લંબાઈવાળા પ્રકાશ માટે એપરચર 1 mm છે, તો ટેલિસ્કોપની વિભેદનશક્તિ ……………………. .
(A) 2.1 × 10-5 rad
(B) 4.1 × 10-5 rad
(C) 5.1 × 10-5 rad
(D) 6.1 × 10-5 rad
જવાબ
(D) 6.1 × 10-5 rad
ટેલિસ્કોપની વિભેદનશક્તિ θ =
∴ θ =
પ્રશ્ન 127.
જીપની હેડલાઈટો વચ્ચેનું અંતર 1.2 m છે. એક વિધાર્થીની ખનો વ્યાસ 2 mm અને
પ્રકાશની તરંગલંબાઈ 5896 Å છે. આ વિધાર્થીને જીપ કેટલાં મહત્તમ અંતરે હોય
ત્યારે તેની બંને હેડલાઈટ અલગ દેખાશે ?
(A) 33.4 km
(B) 33.4 m
(C) 3.34 km
(D) 3.34 m
જવાબ
(C) 3.34 km
વિદ્યાર્થીથી જીપનું અંતર x =
=
3.34 × 103 m = 3.34 km
પ્રશ્ન 128.
માઈક્રોસ્કોપની વિભેદનશક્તિ ………………………
(A) ન્યૂમેરિકલ એપરચરના વ્યસ્ત પ્રમાણમાં છે.
(B) તરંગલંબાઈના સમપ્રમાણમાં છે.
(C) ન્યૂમેરિકલ એપરચરના સમપ્રમાણમાં છે.
(D) ન્યૂમેરિકલ એપરચરથી સ્વતંત્ર છે.
જવાબ
(C) ન્યૂમેરિકલ એપરચરના સમપ્રમાણમાં છે.
ટેલિસ્કોપનું ન્યૂમેરિકલ એપરચર
પ્રશ્ન 129.
પ્રકાશના ધ્રુવીભવનમાં …………………… બદલાય છે.
(A) આવૃત્તિ
(B) તીવ્રતા
(C) તરંગલંબાઈ
(D) કળા
જવાબ
(B) તીવ્રતા
પ્રશ્ન 130.
પ્રકાશ તરંગના પ્રસરણ દરમિયાન દોલન તલ અને ધ્રુવીભવન તલ વચ્ચેનો ખૂણો …………………. હોય છે.
(A) 90°
(B) 60°
(C) 30°
(D) 0°
જવાબ
(A) 90°
પ્રશ્ન 131.
અવીભૂત પ્રકાશ હવામાંથી કાચ (1.5)માં ધ્રુવીભવનકોણે આપાત થાય તો ………………………
(A) પરાવર્તિત કિરણ 100 % ધ્રુવીભૂત છે.
(B) પરાવર્તિત કિરણ 50% ધ્રુવીભૂત છે.
(C) પરાવર્તિત કિરણ અવીભૂત છે.
(D) આમાંથી એક પણ નહીં.
જવાબ
(A) પરાવર્તિત કિરણ 100 % ધ્રુવીભૂત છે.
બ્રુસ્ટરનો નિયમ
પ્રશ્ન 132.
એક પારદર્શક માધ્યમ પર ધ્રુવીભવન કોણ 51॰ છે, તો તે માધ્યમનો વક્રીભવનાંક …………………….. છે.
(A) 0.7771
(B) 0.7547
(C) 1.2349
(D) 1.1504
જવાબ
(C) 1.2349
η = tan θp = tan 51° = 1.2349
પ્રશ્ન 133.
હવામાંથી કાચ પર ………………….. કોણે પ્રકાશ આપાત કરતાં પરાવર્તિત કિરણ સંપૂર્ણ તલધ્રુવીભૂત મળે. (કાચનો વક્રીભવનાંક n છે.)
(A) sin-1 (n)
(B) sin-1 (
(C) tan-1 (
(D) tan-1 (n)
જવાબ
(D) tan-1 (n)
બ્રુસ્ટરના નિયમ પરથી,
n = tan i [∵ θp = i]
∴ i = tan-1(n)
પ્રશ્ન 134.
કાચનો વક્રીભવનાંક 1.6 અને પાણીનો વક્રીભવનાંક 1.33 છે. પાણીમાંથી કાચ પર આપાત પ્રકાશના કિરણ માટે ધ્રુવીભવન કોણ છે.
(A) 49°48′
(B) 39°12′
(C) 39°44′
(D) 50°16′
જવાબ
(D) 50°16′

= tan θp =
∴ θ = tan-1 (1.2030) = 50°16′
પ્રશ્ન 135.
કયા આપાતકોણે કાચના સ્લેબ પરથી પરાવર્તિત પ્રકાશ સંપૂર્ણ તલધ્રુવીભૂત બને ? આ આપાત કોણે વક્રીભૂતકોણ 33.6॰ છે. [2008]
(A) 90°
(B) 0°
(C) 56.4°
(D) 46.4°
જવાબ
(C) 56.4°
θp = 90° – r
= 90° – 33.6° = 56.4°
પ્રશ્ન 136.
પ્રકાશનો હવામાં વેગ 3 × 108 m/s અને કાચમાં વેગ 2 × 108 m/s હોય તો કાચ માટે ધ્રુવીભવનકોણ ………………….. હોય.
(A) 56.50°
(B) 56.30°
(C) 56.1°
(D) 56°
જવાબ
(B) 56.30°
કાચનો વક્રીભવનાંક μ = tanθp
પણ = μ =
∴ θptan-1 (1.5)
∴ θp = 56.30°
પ્રશ્ન 137.
1.55 નિરપેક્ષ વક્રીભવનાંક ધરાવતી કાચની પ્લેટની સપાટી પર પ્રકાશના કિરણને
ધ્રુવીભવનકોણે આપાત કરવામાં આવે છે. આથી વક્રીભૂતકોણ કેટલો થાય ?
(A) 75°11′
(B) 32°49′
(C) 147°11′
(D) 0°
જવાબ
(B) 32°49′

n = tanθp
1.55 = tanθp
∴ θp = tan-1(1.55)
∴ θp = 57° 10′
આકૃતિ પરથી,
θp + 90° + r = 180°
∴ θp + r = 90°
∴ r = 90 – θp
∴ r = 89° 60′ – 57° 10′
∴ r = 32° 50′
પ્રશ્ન 138.
ધ્રુવીભૂતકોણ અને વક્રીભવનાંક વચ્ચે સંબંધ દર્શાવતું સાચું સમીકરણ જણાવો.
(A) μsin θp = 1
(B) μcot θp = 1
(C) μtan θp = 1
(D) μcosec θp = 1
જવાબ
(B) μcot θp = 1
બ્રુસ્ટરના નિયમ પરથી,
μ = tan θp =
μcot θp = 1
પ્રશ્ન 139.
પ્રકાશનું કિરણ એક ગ્લાસની પ્લેટ પર આપાત થાય છે. જ્યારે આપાતકોણ 58° થાય
છે ત્યારે પરાવર્તિત કિરણ સંપૂર્ણ તલધ્રુવીભૂત બને છે, તો કાચનો
વક્રીભવનાંક ………………
(A) 1.6
(B) 1.5
(C) 1.4
(D) 1.35
જવાબ
(A) 1.6
અહીં ધ્રુવીભવનકોણ = આપાતકોણ = θp = 58°
∴ બ્રુસ્ટરના નિયમ પરથી,
માધ્યમનો વક્રીભવનાંક n = tan θp
∴ n = tan 58°
∴ n = 1.6003 ≈ 1.6
પ્રશ્ન 140.
જ્યારે પોલેરૉઇડને ભ્રમણ કરાવવામાં આવે છે, ત્યારે પ્રકાશની તીવ્રતામાં
વધઘટ થાય છે, પરંતુ ક્યારેય શૂન્ય થતી નથી. આથી કહી શકાય કે આપાત પ્રકાશ
…………………. છે.
(A) સંપૂર્ણ ધ્રુવીભૂત
(B) અંશતઃ ધ્રુવીભૂત
(C) અમ્બુવીભૂત
(D) એક પણ નહીં
જવાબ
(B) અંશતઃ ધ્રુવીભૂત
અંશતઃ ધ્રુવીભૂત પ્રકાશના માર્ગમાં પોલેરૉઇડ ગોઠવીને ભ્રમણ આપતા નિર્ગમન
પ્રકાશમાં હંમેશાં કોઈક પ્રકાશ સદિશો હાજર હોવાથી તીવ્રતા શૂન્ય મળે નહીં.
પ્રશ્ન 141.
કોઈ એક માધ્યમ માટે ક્રાંતિકોણ sin-1(0,6) છે, તો આ માધ્યમ માટે ધ્રુવીભવનકોણ …………………..
(A) sin-1(0.8)
(B) sin-1(1.5)
(C) tan-1(1.6666)
(D) tan-1(0.6)
જવાબ
(C) tan-1(1.6666)
ક્રાંતિકોણ C = sin-1(0.6)
∴ sinC = 0.6
∴
∴ n =
∴ tanθp =
∴ θp = tan-1(
∴ θp = tan-1(1.6666)
પ્રશ્ન 142.
પાણીમાં ગતિ કરતું પ્રકાશનું કિરણ પાણીમાં ડુબાડેલ ગ્લાસ પ્લેટ પર આપાત થાય
છે, જ્યારે આપાતકોણ 51° નો બને છે ત્યારે પરાવર્તિત કિરણ સંપૂર્ણ
તલધ્રુવીભૂત બને છે, તો કાચનો વક્રીભવનાંક કેટલો થશે ? (પાણીનો વક્રીભવનાંક
1.3 અને tan 51° = 1.235) [2008]
(A) 1.33
(B) 1.805
(C) 1.605
(D) 1.305
જવાબ
(C) 1.605
∴ ng = nwtan51°
= 1.3 × 1.235
= 1.6055 ≈ 1.605
પ્રશ્ન 143.
કોઈ એક માધ્યમ માટે ધ્રુવીભવનકોણ 60° છે, તો તેના માટે ક્રાંતિકોણ કેટલો ?
(A) sin-1(
(B) tan-1√3
(C) cos-1(
(D) tan-1(
જવાબ
(A) sin-1
μ = tanθp = tan60°
∴ μ =
ક્રાંતિકોણ
sinC =
∴ C = sin-1(
પ્રશ્ન 144.
આકૃતિમાં AO આપાતકિરણ છે. ગ્લાસના સ્લેબનો વક્રીભવનાંક 1.54 છે. પરાવર્તિત
કિરણ OB ના માર્ગમાં નિકોલ પ્રિઝમ યોગ્ય રીતે ગોઠવ્યો છે, હવે નિકોલ
પ્રિઝમને યોગ્ય ભ્રમણ આપતા તેમાંથી બહાર આવતા પ્રકાશની તીવ્રતા ……………………..
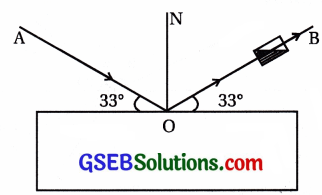
(A) શૂન્ય થઈ જાય છે અને શૂન્ય જ રહે છે.
(B) તીવ્રતા થોડીક ઘટે છે અને થોડીક વધે છે.
(C) તીવ્રતામાં કોઈ ફેરફાર થતો નથી.
(D) તીવ્રતા ક્રમશઃ ઘટીને શૂન્ય થાય છે અને પછી વધે છે.
જવાબ
(D) તીવ્રતા ક્રમશઃ ઘટીને શૂન્ય થાય છે અને પછી વધે છે.
પ્રશ્ન 145.
એકબીજાની ઉપર મૂકેલા પોલેરાઇઝર પર અધ્રુવીભૂત પ્રકાશ આપાત થાય છે, તો આ
બંને પોલેરાઇઝરની વચ્ચે કેટલો કોણ હોવો જોઈએ કે જેથી પારગમન પામતા પ્રકાશની
તીવ્રતા
આપાત પ્રકાશકિરણની તીવ્રતા કરતાં
(A) 54.7°
(B) 35.3°
(C) 0°
(D) 60°
જવાબ
(B) 35.30
ધારોકે આપાતપ્રકાશની તીવ્રતા I0 છે.
∴ પ્રથમ પોલેરાઇઝરમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I1 હોય તો,
I1 = I0cos2θ
=
હવે, બીજા પોલે૨ાઇઝરમાંથી નિર્ગમન પામતા પ્રકાશની
તીવ્રતા I2 =
∴ I2 = I1cos2θ’
∴
∴ cosθ’ =
∴sin(90° – θ’) = 0.8165
∴ 90° – θ’ = 54.7°
∴ θ’ = 90° – 54.7° ∴ θ’ = 35.3°
પ્રશ્ન 146.
સામાન્ય પ્રકાશ ગ્લાસના ચોસલા પર પોલેરાઇઝિંગ કોણે આપાત થઈ 22° જેટલું વિચલન અનુભવે છે, તો વક્રીભૂતકોણ …………………… હશે. (CET – 1998)
(A) 74°
(B) 22°
(C) 90°
(D) 34°
જવાબ
(D) 34°

આકૃતિ પરથી, θp = r + 22° ………. (1)
હવે બ્રુસ્ટરના નિયમની સાબિતી પરથી,
θp + 90° + r = 180°
∴ પરિણામ (1) પરથી,
r + 22° + r = 90°
∴ 2r = 68° ∴ r = 34°
પ્રશ્ન 147.
એક વ્યક્તિ તળાવના શાંત પાણી પરથી પરાવર્તિત થયેલો સૂર્યનો તલઘુવીભૂત
પ્રકાશ મેળવે છે. જો પાણીનો વક્રીભવનાંક 1.327 હોય તો, સૂર્ય ક્ષિતિજથી
કેટલા કોણે હશે ?
(A) 57°
(B) 75°
(C) 37°
(D) 53°
જવાબ
(C) 37°

બ્રુસ્ટરનાં નિયમ પરથી, n = tanθp
1.327 = tanθp
∴ θp = 53°
ક્ષિતિજ સાથે સૂર્યએ બનાવેલ કોણ = 90° – θp
= 90° – 53°
= 37°
પ્રશ્ન 148.
I0 તીવ્રતાવાળા અધ્રુવીભૂત પ્રકાશના માર્ગમાં બે પોલેરોઇડ એવી
રીતે મૂકેલ છે કે જેથી બીજા પોલેરોઇડમાંથી પ્રકાશ નિર્ગમન પામતો નથી. જો આ
બે પોલેરૉઇડની વચ્ચે ત્રીજો પોલેરૉઇડ, પ્રથમ પોલેરૉઇડની દ-અક્ષ સાથે θ ખૂણે
મૂકવામાં આવે તો છેલ્લા પોલેરૉઇડમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
…………………
(A) (
(B) (
(C) (
(D) I0cos4 θ
જવાબ
(A) (

P1 માંથી બહાર આવતા પ્રકાશની તીવ્રતા =
જો P3 પર આપાત પ્રકાશની તીવ્રતા
I1 =
હવે, P2 પર આપાત પ્રકાશની તીવ્રતા I1 =
તેમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા I2 હોય તો,
I2 = I1cos2(90° – θ) = I1sin2θ
I2 =
=
=
∴ I2 =
પ્રશ્ન 149.
બે નિકોલ પ્રિઝમના મુખ્ય સમતલો વચ્ચેનો ખૂણો 60° છે. આ પ્રિઝમ પર અધ્રુવીભૂત પ્રકાશ આપાત કરતાં ………………….. પ્રકાશ નિર્ગમન પામશે.
(A) 50
(B) 100
(C) 37.5
(D) 12.5
જવાબ
(D) 12.5
પ્રથમ નિકોલ પ્રિઝમમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I1 =
બીજા નિકોલ પ્રિઝમમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I2 = I1cos2θ
=
=
=
પ્રશ્ન 150.
ટુર્મેલિન પ્લેટ પર તલઘુવીભૂત પ્રકાશ આપાત થાય છે. આ પ્લેટની દક્-અક્ષ સાથે
(A) 19%
(B) 92%
(C) 50%
(D) 29%
જવાબ
(C) 50%
I = I0cos245°
∴ I = I0 ×
∴
=
પ્રશ્ન 151.
પારદર્શક માધ્યમ પર જ્યારે ધ્રુવીભવનકોણે પ્રકાશ આપાત થાય ત્યારે પરાવર્તિત કિરણમાં …………………….. ઘટકો હોય છે.
(A) માત્ર 15% σ ઘટકો
(B) માત્ર 15% π ઘટકો
(C) 85% σ ઘટકો અને 15% π ઘટકો
(D) 85% π ઘટકો અને 100% σ ઘટકો
જવાબ
(A) માત્ર 15% σ ઘટકો
પ્રશ્ન 152.
60° ના કોણે આપાત થતાં કિરણ માટે પરાવર્તિત કિરણ સંપૂર્ણ તલધ્રુવીભૂત થાય
છે, તો ઘટ્ટ માધ્યમમાં વક્રીભૂત પામતા કિરણનો વેગ …………………… ms-1 મળે.
(A) √2
(B) √3 × 108
(C) √3
(D) √2 × 108
જવાબ
(B) 3√ × 108
n = tanθp = tan60°
∴ v =
પ્રશ્ન 153.
પાંચ પોલેરૉઇડને એકબીજાને સ્પર્શે તે રીતે ગોઠવીને એક તંત્ર બનાવ્યું છે.
દરેકની સમાન અક્ષને એક પછી એક પોલેરોઇડને 60° નું ભ્રમણ આપવામાં આવે છે. તો
છેલ્લા પોલેરૉઇડમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા, આપાત પ્રકાશની
તીવ્રતાનો ………………….. ભાગ હશે.
(A)
(B)
(C)
(D)
જવાબ
(D)
ધારો કે પોલેરૉઇડ પર આપાત પ્રકાશની તીવ્રતા I0 છે.
તેમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I1 =
બીજા પોલેરૉઇડમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I2 =
=
ત્રીજા પોલેૉઇડમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I3 =
ચોથા પોલેરૉઇડમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I4 =
પાંચમા પોલેરૉઇડમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I5 =
બીજી ટૂંકી રીતે :
I5 =
પ્રશ્ન 154.
જ્યારે અવીભૂત પ્રકાશ કે જેની ઊર્જા 3 × 10-3J છે, તેને 3 × 10-4 m2 ક્ષેત્રફળવાળા પોલેરાઈઝર પર આપાત થાય છે. પોલેરાઈઝર 3.14 rad s-1 ની કોણીય ઝડપ ભ્રમણ કરે છે, તો તેના 1 પરિભ્રમણ દીઠ નિર્ગમન પામતી ઊર્જા શોધો.
(A) 47.1 × 10-4 J
(B) 27.1 × 10-4 J
(C) 37.1 × 10-4 J
(D) 17.1 × 104 J
જવાબ
(A) 47.1 × 10-4 J
ω = 3.14 rad s-1
∴ T =
∴ T = 2 s

એક પરિભ્રમણ દીઠ નિર્ગમન પામતી ઊર્જા
E = × ક્ષેત્રફળ × કોણીય ઝડપ
=
પ્રશ્ન 155.
બે પોલેરૉઇડ ક્રૉસ્ડ સ્થિતિમાં છે અને નિર્ગમન પામતા પ્રકાશની તીવ્રતા
શૂન્ય છે. જો ત્રીજો પોલેરૉઇડ આ બંનેની દક્-અક્ષ વચ્ચેના ખૂણા કરતાં અડધાં
ખૂણે બંનેની વચ્ચે મૂકવામાં આવે, તો નિર્ગમન પામતા પ્રકાશની તીવ્રતા
………………………. થાય. જ્યાં I0 આપાત પ્રકાશની મહત્તમ તીવ્રતા છે.
(A)
(B)
(C) I0
(D)
જવાબ
(D)
પ્રથમ પોલેરૉઇડ પર આપાત પ્રકાશની તીવ્રતા I0 હોય તો
તેમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા I1 =
હવે બીજા પોલેરૉઇડ પર આપાત પ્રકાશની તીવ્રતા I1 છે. તેથી
તેમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I” =
પ્રશ્ન 156.
ચોક્કસ માધ્યમ માટે ક્રાંતિકોણ sin-1(
(A) sin-1(
(B) tan-1(
(C) tan-1(
(D) tan-1(
જવાબ
(B) tan-1(
θ = sin-1(
∴ sinθ =
∴
∴ n =
હવે બ્રુસ્ટરના નિયમ પરથી,
n = tanθp
∴ θp = tan-1(n)
∴ θp = tan-1(
પ્રશ્ન 157.
આપણી સાપેક્ષે આકાશગંગાએ કેટલી ઝડપથી ગતિ કરવી જોઈએ કે જેથી 589.0 nmની સોડિયમ રેખા 589.6 nm આગળ દેખાય ?
(A) 306 × 10-3m/s
(C) 306 × 103 m/s
(B) 305 × 103 m/s
(D) 306 × 103km/s
જવાબ
(C) 306 × 103 m/s
v = c હોવાથી,

= 0.003056 × 108
= 306 × 103 m/s
તેથી આકાશગંગા આપણાથી 306 km/s ના વેગથી દૂર જાય છે.
આપણી સાપેક્ષે આકાશગંગાએ કેટલી ઝડપથી ગતિ કરવી જોઈએ કે જેથી 6000 nmની સોડિયમ રેખા 605,0 nm આગળ દેખાય ?
(જવાબ : v = 2.5 × 106 ms-1)
પ્રશ્ન 158.
બે લિટો વચ્ચેનું અંતર 1 mm અને પડદો 1 m દૂર રાખવામાં આવેલ છે. જ્યારે 500
nm તરંગલંબાઈનો બ્લૂ-ગ્રીન પ્રકાશ વાપરવામાં આવે ત્યારે શલાકાઓ વચ્ચેનું
અંતર કેટલું હશે ?
(A) 5 × 1010 m
(B) 5 × 10 4 m
(C) 5 × 10-6 m
(D) 5 × 10-7 m
જવાબ
(B) 5 × 10-4m
બે ક્રમિક શલાકા વચ્ચેનું અંતર,
β =
D = 1m,
d = 1mm = 10-3m
λ = 500nm = 5 × 10-7 m
∴ β =
= 5 × 10-4 m
≈ 0.5 × 10-3 m = 0.5 mm
બે સ્લિટો વચ્ચેનું અંતર 1.33 mm અને પડદો 1.33 m દૂર રાખવામાં આવેલ છે. જ્યારે 630 nm તરંગલંબાઈનો બ્લૂ- ગ્રીન પ્રકાશ વાપરવામાં આવે ત્યારે શલાકાઓ વચ્ચેનું અંતર કેટલું હશે ? (જવાબ : β = 0.63 mm)
પ્રશ્ન 159.
એવું ધારો કે તારામાંથી 6000 Å તરંગલંબાઈનો પ્રકાશ આવે છે, જેનાં
ઓબ્જેક્ટિવનો વ્યાસ 100 ઇંચ હોય તેવા ટેલિસ્કોપ માટે વિભેદનની સીમા શું હશે
?(માર્ચ 2020, ઑગષ્ટ 2020)
(A) 2.9 rad
(B) 2.9 × 10-7 rad
(C) 2.9 × 10-5 rad
(D) 2.9 × 10-9 rad
જવાબ
(B) 2.9 × 10-7rad
ટેલિસ્કોપના ઑબ્જેક્ટિવનો વ્યાસ 2a = 100 ઇંચ
પણ 1 ઇંચ = 2.54 cm
∴ 24 = 100 × 2.54
= 254 cm
∴ a = 127 cm
અને તરંગલંબાઈ λ = 6000 Å = 6000 × 10-8 cm
∴λ = 6 × 10-5 cm
ટેલિસ્કોપની વિભેદન સીમા,
Δθ =
=
Δθ ≈ 2.9 × 10-7 રેડિયન
એવું ધારો કે તારામાંથી 6000 Å તરંગલંબાઈનો પ્રકાશ આવે છે. જેનાં ઑબ્જેક્ટિવનો વ્યાસ 80 ઇંચ હોય તેવા ટેલિસ્કોપ માટે વિભેદનની સીમા શું હશે ?(જવાબ : Δθ = 3.6 × 10-7 રેડિયન)
પ્રશ્ન 160.
જ્યારે અડચણની પહોળાઈ ૩ mm હોય અને તરંગલંબાઈ 500 nm હોય તો કયા અંતર માટે કિરણ પ્રકાશશાસ્ત્ર એક સારી સંનિકટતા હશે ? (ઑગષ્ટ 2020)
(A) 6 m
(B) 18mm
(C) 18 m
(D) 6 mm
જવાબ
(C) 18 m
અહીં અડચણની પહોળાઈ a = 3mm = 3 × 10-3m
તરંગલંબાઈ λ = 500 nm = 5 × 10-7 m
⇒ ફ્રેનલ લંબાઈ,
Zf =
∴ Zf =
∴ Zf = 18 m
આ દર્શાવે છે કે જ્યારે તરંગો ઘણા મીટર લાંબા હોય ત્યારે નાના અડચણ માટે
વિવર્તનને કારણે થતો ફેલાવો અવગણી શકાય. આમ, ઘણી સામાન્ય પરિસ્થિતિઓમાં
કિરણ પ્રકાશશાસ્ત્ર લાગુ પાડી શકાય છે.
જ્યારે અડચણની પહોળાઈ 4 mm હોય અને તરંગલંબાઈ 800 nm હોય તો ક્યા અંતર માટે કિરણ પ્રકાશશાસ્ત્ર એક સારી સંનિકટતા હશે ? (જવાબ : Zf = 20 m)
પ્રશ્ન 161.
અવીભૂત પ્રકાશ એક સમતલ કાચની સપાટી પર આપાત થાય છે. પરાવર્તિત અને વક્રીભૂત
કિરણો એકબીજાને લંબ થાય તે માટે કેટલો આપાતકોણ હશે ? (ઓગષ્ટ 2020)
(A) 33°
(B) 57°
(C) 24°
(D) આમાંથી એક પણ નહીં
જવાબ
(B) 57°
અહીં પરાવર્તિત અને વક્રીભૂત કિરણો એકબીજાને લંબ થાય.
જો આપાતકોણ i અને વક્રીભૂતકોણ r હોય તો,
i + r =
અને આ આપાતકોણને બ્રુસ્ટરકોણ કહે છે તેથી i = iB.
હવે સ્નેલના નિયમ પરથી,
μ =
∴ μ = tan iB
પણ કાચ માટે વક્રીભવનાંક μ = 1.5
∴1.5= tan iB
∴ iB = tan-1 (1.5) ∴ iB = 56° 19′
∴ iB ≈ 57°
જે હવા અને કાચના આંતરપૃષ્ઠ માટેનો બ્રુસ્ટરકોણ છે.
પ્રશ્ન 162.
589 nm તરંગલંબાઈ ધરાવતો એકરંગી પ્રકાશ હવામાંથી પાણીની સપાટી ઉપર આપાત થાય
છે, તો પરાવર્તિત પ્રકાશની આવૃત્તિ કેટલી હશે ? પ્રકાશની પાણીમાં ઝડપ 3 ×
10m/s છે.
(A) 5.09 × 1014 Hz
(B) 1.7 × 10-19 Hz
(C) 5.09 × 1017 Hz
(D) 1.7 × 10-14 Hz
જવાબ
(A) 5.09 × 1014 Hz
પ્રકાશની હવામાં તરંગલંબાઈ λ = 589 nm = 589 × 10-9 m
હવામાં ઝડપ c = 3 × 108 m/s
પાણીનો વક્રીભવનાંક μw = 1.33
(a) પરાવર્તિત પ્રકાશ માટે, ઝડપ અને તરંગલંબાઈ, આપાત પ્રકાશની ઝડપ અને તરંગલંબાઈ જેટલી હોય.
∴ ઝડપ c = 3 × 108 m/s અને
તરંગલંબાઈ λ = 589 × 10-9 m
તથા આવૃત્તિ v =
∴ V = 0.00509 × 1017 Hz
∴ V × 5.09 × 1014 Hz
પ્રશ્ન 163.
589 nm તરંગલંબાઈ ધરાવતો એકરંગી પ્રકાશ હવામાંથી પાણીની સપાટી પર આપાત થાય
છે, તો વક્રીભૂત પ્રકાશની તરંગલંબાઈ કેટલી ? પ્રકાશની પાણીમાં ઝડપ = 2.26 ×
108 m/s અને 5.09 × 1014 Hz આવૃત્તિ છે.
(A) 444 nm
(B) 226 nm
(C) 509 nm
(D) 589 nm
જવાબ
(A) 444 nm
પ્રકાશની હવામાં તરંગલંબાઈ λ = 589 nm = 589 × 10-9 m
હવામાં ઝડપ c = 3 × 108 m/s
પાણીનો વક્રીભવનાંક μw = 1.33
(b) વક્રીભૂત પ્રકાશ માટે આવૃત્તિ અચળ રહે અને તરંગલંબાઈ તથા ઝડપ બદલાય.
∴ આવૃત્તિ v = 5.09 × 1014 Hz
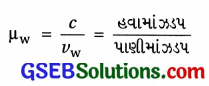
∴ uw =
= 2.2556 × 108
≈ 2.26 × 108 m/s
અને તરંગલંબાઈ,
λw =
∴ λw = 0.444 × 10-6
∴ λw ≈ 444 × 10-9 m
પ્રશ્ન 164.
કાચનો વક્રીભવનાંક 1.5 છે. પ્રકાશની કાચમાં ઝડપ કેટલી હશે ? (શૂન્યાવકાશમાં પ્રકાશની ઝડપ 3.0 × 108 ms-1 છે)
(A) 5 × 10-19 ms-1
(B) 5 × 108 m/s
(C) 2 × 108 m/s
(D) 2 × 10-8 m/s
જવાબ
(C) 2 × 108m/s
(a) અહીં μ = 1.5, c = 3.0 × 108 ms-1

પ્રશ્ન 165.
યંગના બે-સ્લિટના પ્રયોગમાં, બે સ્લિટો વચ્ચેનું અંતર 0.28 mm અને પડદો
1.4m દૂર મૂકેલો છે. મધ્યસ્થ પ્રકાશિત શલાકા અને ચોથી પ્રકાશિત શલાકા
વચ્ચેનું અંતર 1.2 cm જેટલું માપવામાં આવે છે. પ્રયોગમાં વપરાયેલ પ્રકાશની
તરંગલંબાઈ શોધો.
(A) 4000 Å
(B) 5000 Å
(C) 6000 Å
(D) 7000 Å
જવાબ
(C) 6000 Å
અહીં બે સ્લિટ વચ્ચેનું અંતર d = 0.28 mm 28 × 10-3 cm સ્વિટો અને પડદા વચ્ચેનું અંતર D = 1.4m = 140 cm મધ્યસ્થ પ્રકાશિત અને ચોથી પ્રકાશિત શલાકા વચ્ચેનું અંતર
x4 = 1.2 cm
⇒ ‘n’ મી પ્રકાશિત શલાકાનું સ્થાન,
xn =
∴ x4 =
λ =
∴ λ = 6000 × 10-8 cm
∴ λ = 6000 Å [∵ 10-8 cm = 1 Å]
પ્રશ્ન 166.
યંગના બે લિટના પ્રયોગમાં વ્યતિકરણ શલાકાઓ મેળવવા માટે 650 1m તરંગલંબાઈ
ધરાવતાં પ્રકાશ માટે પડદા પર મળતી ત્રીજી પ્રકાશિત શલાકાનું મધ્યસ્થ
અધિકતમના મધ્યબિંદુથી અંતર શોધો.
(A) 7.8 mm
(B) 1.95 mm
(C) 5.2 mm
(D) 1.17mm
જવાબ
(D) 1.17mm
અહીં, d = 2 mm = 2 × 10-3 m
D = 120 cm = 1.2 m
λ1 = 650 nm = 65 × 10-8 m
λ2 = 520 nm = 52 × 10-8 m
(a) λ1 તરંગલંબાઈવાળા પ્રકાશ માટે મધ્યસ્થ અધિકતમથી ત્રીજી પ્રકાશિત શલાકાનું અંતર,
x3 =
= 117 × 10-5 = 1.17 × 10-3 m
∴ x3 = 1.17 mm
પ્રશ્ન 167.
બે-લિટના પ્રયોગમાં 1 m દૂર મૂકેલા પડદા પર એક શલાકાની કોણીય પહોળાઈ 0.2°
મળે છે. વપરાયેલ પ્રકાશની તરંગલંબાઈ 600 nm છે, જો આખાય પ્રાયોગિક સાધનને
પાણીમાં ડૂબાડવામાં આવે તો તે શલાકાની કોણીય પહોળાઈ કેટલી થશે ? પાણીનો
વક્રીભવનાંક
(A) 0.27°
(B) 0.15°
(C) 0.2°
(D) 0.21°
જવાબ
(B) 0.15°
સ્કિટોથી D અંતરે રાખેલા પડદા પર રચાતી શલાકાની પહોળાઈ β હોય તો, કોણીય પહોળાઈ,
θ =
∴ d =
⇒ જો પાણીમાં તરંગલંબાઈ λ’ અને કોણીય પહોળાઈ 8′ હોય તો,
∴ d =
∴ સમીકરણ (1) અને (2) પરથી,
∴ θ’ = θ ×
પણ વક્રીભવનાંક μ =
∴ θ’ = θ ×
(નોંધ : જો વિવર્તન ભાતની મધ્યસ્થ અધિકતમની પહોળાઈ માંગે તો આ પહોળાઈ =
∴ θ’ =
પ્રશ્ન 168.
હવામાંથી કાચમાં જતા પ્રકાશ માટે બ્રુસ્ટર કોણ કેટલો હશે ? (કાચનો વક્રીભવનાંક = 1.5).
(A) 53.6°
(B) 35.3°
(C) 56.3°
(D) 36.5°
જવાબ
(C) 56.3°
બ્રુસ્ટરના નિયમ પરથી,
taniβ = μ
∴ iβ = tan-1(μ)
∴ iβ = tan-1(1.5)
∴ iβ = 56.3°
નોંધ : જો વક્રીભૂતકોણ માંગેલ હોત તો,
r = 90° – iB = 90° – 56.3°, r = 33.7°
પ્રશ્ન 169.
એક સમતલ પરાવર્તક સપાટી ઉપર 5000 Å તરંગલંબાઈનો પ્રકાશ આપાત થાય છે, તો કયા આપાતકોણે પરાવર્તિત કિરણ એ આપાતકિરણને લંબ થશે ?
(A) 90°
(B) 45°
(C) 135°
(D) 60°
જવાબ
(B) 45°
આપાત પ્રકાશની તરંગલંબાઈ અને આવૃત્તિ (ઝડપ) જેટલી જ પરાવર્તિત પ્રકાશની તરંગલંબાઈ અને આવૃત્તિ (ઝડપ) હોય છે.
∴ પરાવર્તિત પ્રકાશની તરંગલંબાઈ = 5000 Å

v =
∴ v = 0.6 × 1015 Hz
∴ v = 6 × 1014 Hz
હવે પરાવર્તનના નિયમ પરથી,
આપાતકોણ i પરાવર્તનકોણ r
પણ પરાવર્તિત કિરણ, આપાતિકરણને લંબ છે.
∴ i + r = 90°
∴ i + i = 90° [∵ i = r]
∴ 2i = 90°
∴ i = 45°
પ્રશ્ન 170.
એક તારામાં હાઇડ્રોજન દ્વારા ઉત્સર્જિત 6563 ની Hα રેખા 15 Å જેટર્જી Red-Shift થયેલી જણાય છે. તારાની પૃથ્વીથી દૂર જવાની ઝડપનો અંદાજ શોધો.
(A) 686 × 105 ms-1
(B) – 686 × 105 ms-1
(C) 6.86 × 105 ms-1
(D) – 6.86 × 105 ms-1
જવાબ
(D) – 6.86 × 105ms-1
અહીં λ = 6563 Å, Δλ = 15 Å
હવે પ્રકાશ માટેની ડૉપ્ટર અસર પરથી,
∴ v = –
=  × 3 × 108
× 3 × 108
= – 0.0068566 × 108
∴ v ≈ – 6.86 × 105 m/s-1
ઋણ ચિહ્ન સૂચવે છે કે તારો પૃથ્વીથી દૂર જાય છે.
પ્રશ્ન 171.
600 nm તરંગલંબાઈ ધરાવતા પ્રકાશની મદદથી કરેલ બે-સ્લિટના પ્રયોગમાં, દૂર
રાખેલા પડદા પર મળેલ શલાકાની કોણીય પહોળાઈ 0.1° મળે છે. બે સ્લિટો વચ્ચેનું
અંતર કેટલું હશે ?
(A) 3.44 × 10-4m
(B) 955 m
(C) 3.44 × 104 m
(D) 3.44 × 104 cm
જવાબ
(A) 3.44 × 10-4 m
સ્વિટથી D અંતરે રહેલા પડદા પર β પહોળાઈની શલાકા રચાય તો,
θ =
∴ θ =
∴ θ =
પણ અહીં λ = 600 nm = 6 × 10-7 m
θ = 0.1° =
∴
∴ d =
∴ d = 3439.4 × 10-7 = 3.44 × 10-4 m
પ્રશ્ન 172.
બે ટેકરીઓ પર રહેલા બે ટાવરો એકબીજાથી 40 km દૂર છે. તેમને જોડતી રેખા,
બરાબર વચ્ચે આવેલી ટેકરીની 50 m ઉપરથી પસાર થાય છે. નોંધપાત્ર વિવર્તન અસરો
સિવાય બે ટાવરો વચ્ચે મોકલી શકાય તેવા રેડિયોતરંગોની સૌથી વધુ તરંગલંબાઈ
કેટલી હશે ?
(A) 125 cm
(B) 12.5 cm
(C) 1.25 cm
(D) 0.125 cm
જવાબ
(B) 12.5 cm
- અહીં બે ટેકરીઓ વચ્ચેનું અંતર D = 40 km
બે ટેકરીઓના મધ્યમાંથી કોઈ એક ટેકરીનું અંતર એટલે ફ્રેનલ અંતર Zf =D2=402 = 20 km - બે ટેકરીઓની મધ્યમાં આવેલી ટેકરી (અડચણ)ની સાઇઝ,
a = 50 m
હવે,
Zf =a2λ˙
λ =a2Zf
=(50)220000=250020000
∴ λ = 0.125 m
∴ λ = 12.5 cm
પ્રશ્ન 173.
500 nm તરંગલંબાઈ ધરાવતું સમાંતર પ્રકાશ કિરણપૂંજ એક સાંકડી સ્લિટ પર પડે
છે અને પરિણામી વિવર્તનભાત 1 m દૂર રાખેલા પડદા ઉપર જોવામાં આવે છે. એવું
જોવા મળે છે કે, પ્રથમ ન્યૂનતમ પડદાના કેન્દ્રથી 2.5 mm અંતરે આવેલ છે.
સ્લિટની પહોળાઈ શોધો.
(A) 0.02 mm
(B) 0.2 mm
(C) 2.0 mm
(D) 0.002 mm
જવાબ
(B) 0.2 mm
અહીં D = 1m, n = 1 (ન્યૂનતમ)
x1 = 2.5 mm = 2.5 × 10-3 m
λ = 500 nm = 5 × 10-7 m
⇒ nમાં ક્રમના ન્યૂનતમ માટેની શરત,
xn =
xn =
∴ d =
∴ d = 2 × 10-4 m = 0.2 × 10-3 m
∴ d = 0.2 mm
પ્રશ્ન 174.
સ્થિર વ્યતિકરણની ઘટનાના નિદર્શન માટે વિકિરણોનું ઉત્સર્જન કરતાં બે ઉદ્ગમો કેવા હોવા જોઈએ ? (2003)
(A) લગભગ સમાન આવૃત્તિવાળા
(B) સમાન આવૃત્તિવાળા
(C) જુદી જુદી તરંગલંબાઈવાળા
(D) સમાન આવૃત્તિવાળા તથા નિશ્ચિત કળાતફાવતવાળા
જવાબ
(D) સમાન આવૃત્તિવાળા તથા નિશ્ચિત કળાતફાવતવાળા
સ્થિર વ્યતિકરણ માટે બે ઉદ્ગમો સુસમ્બદ્ધ હોવા જોઈએ અને સુસમ્બદ્ધ ઉદ્ગમો માટે આવૃત્તિ સમાન અને કળાતફાવત શૂન્ય અથવા અચળ હોવા જોઈએ.
પ્રશ્ન 175.
હવામાંથી કાચ પર ……………………… કોણે પ્રકાશ આપાત કરતાં પરાવર્તિત કિરણ સંપૂર્ણ તલધ્રુવીભૂત મળે. (કાચનો વક્રીભવનાંક n છે.)
(2004)
(A) sin-1 (n)
(B) sin-1 (
(C) tan-1 (
(D) tan-1 (n)
જવાબ
(D) tan-1 (n)
બ્રુસ્ટરના નિયમ પરથી,
n = tan i [∵ θp = i ]
∴ i = tan-1 (n)
પ્રશ્ન 176.
યંગના સ્થિર વ્યતિકરણના પ્રયોગમાં બે સ્લિટો વચ્ચેનું અંતર, તરંગલંબાઈ
કરતાં બમણું હોય (d = 2λ) ત્યારે પડદા પર વધુમાં વધુ ………………. પ્રકાશિત
શલાકાઓ રચાય. (2004)
(A) અનંત
(B) પાંચ
(C) ત્રણ
(D) શૂન્ય
જવાબ
(B) પાંચ
‘n’મા ક્રમની પ્રકાશિત શલાકા માટે પથતફાવત
d sinθ = nλ
∴ sinθ =
∴ sinθ =
પણ sinθ નો વિસ્તાર (−1, 1) છે.
∴ sinθ ≤ 1
∴ n ≤ 2
∴ n નાં શક્ય મૂલ્યો -2, -1, 0, 1, 2. આમ, પડદા પર એક મધ્યસ્થ અધિકતમ, તેની
બંને બાજુ પ્રથમ ક્રમની બે અને બીજા ક્રમની બે એમ મળીને કુલ પાંચ પ્રકાશિત
શલાકાઓ મળે.
પ્રશ્ન 177.
યંગના ડબલ સ્લિટ પ્રયોગમાં એકરંગી પ્રકાશનું ઉદ્ગમ વાપરવામાં આવે ત્યારે પડદા પર ………………………… આકારની શલાકાઓ મળે. (2005)
(A) અતિવલય
(C) સુરેખ
(B) વર્તુળ
(D) પરવલય
જવાબ
(C) સુરેખ
અત્રે બંને સ્લિટો રેખીય ઉદ્ગમો તરીકે વર્તે છે તેથી પડદા પર જુદા જુદા બિંદુઓએ મળતી શલાકાઓ પણ સુરેખ જ હોય.
પ્રશ્ન 178.
I0 જેટલી તીવ્રતાવાળા અધ્રુવીભૂત પ્રકાશને ધ્રુવીભવન પ્લેટ પર આપાત કરતાં તેમાંથી બહાર ન આવતા પ્રકાશની તીવ્રતા ……………………… હશે. (2005)
(A) શૂન્ય
(B) I0
(C)
(D)
જવાબ
(C)
ધ્રુવીભૂત પામતા પ્રકાશની તીવ્રતા =
બહાર ન આવતા પ્રકાશની તીવ્રતા = I –
પ્રશ્ન 179.
પડદા પર એકબીજાથી 1 mm અંતરે રહેલાં બે પ્રકાશિત બિંદુઓ છે. જેને કોઈ એક
વ્યક્તિ જુએ છે. વ્યક્તિની આંખની કીકીનો વ્યાસ 3 mm છે. કયા મહત્તમ અંતરથી
વ્યક્તિ આ બિંદુઓને સ્પષ્ટપણે છૂટાં જોઈ શકશે ? (પ્રકાશની તરંગલંબાઈ = 500
nm) (2005)
(A) 6m
(B) 3m
(C) 5m
(D) 1m
જવાબ
(C) 5 m

પ્રશ્ન 180.
એક લિટથી થતાં એકરંગી પ્રકાશના, ફ્રોનહોફર વિવર્તનમાં મધ્યસ્થ અધિકતમની તીવ્રતા I0 છે. જો તે સ્વિટની પહોળાઈ બમણી કરવામાં આવે તો મધ્યસ્થ અધિકતમ તીવ્રતા ……………………… મળશે. (2005)
(A) I0
(B)
(C) 2I0
(D) 4I0
જવાબ
(A) I0
θ જેટલા વિવર્તનકોણે પડદા પર મળતી તીવ્રતા,

ટૂંકી રીતે :
અધિકતમની તીવ્રતા પ્રકાશના ઉદ્ગમ પર આધારિત છે. અત્રે પ્રકાશનું ઉદ્ગમ બદલાતું નથી તેથી અધિકતમ તીવ્રતા પણ બદલાય નહિ.
પ્રશ્ન 181.
યંગના ડબલ સ્લિટના પ્રયોગમાં કોઈ એક બિંદુએ તીવ્રતા I અને થતફાવત છે, જ્યાં λ એ પ્રકાશની તરંગલંબાઈ
(A)
(B)
(C)
(D)
જવાબ
(D)
મહત્તમ તીવ્રતા I0 = I’ + I’ + 2
= 21′ + 2I’ [∵ cos0° = 1]
= 4I’
અને કોઈ બિંદુએ તીવ્રતા I = I’ + I’ + 2
જ્યાં Φ =
=
∴ I = 2I’ + 2I’cos
= 2I’ + I’ = 3I’
∴
પ્રશ્ન 182.
યંગના ડબલ સ્લિટના પ્રયોગમાં 590 nm તથા અજ્ઞાત તરંગલંબાઈવાળા પ્રકાશનું
મિશ્રણ વાપરતાં પડદા પર મળતી વ્યતિકરણ ભાતોમાં બંને પ્રકાશની મધ્યસ્થ
અધિકતમ શલાકાઓ એકબીજા પર સંપાત થાય છે. વળી પડદા પર કોઈ સ્થાને 590 nm
તરંગલંબાઈવાળા પ્રકાશની ત્રીજી પ્રકાશિત શલાકા, અજ્ઞાત તરંગલંબાઈવાળા
પ્રકાશની ચોથી પ્રકાશિત શલાકા પર સંપાત થાય છે, તો આ અજ્ઞાત તરંગલંબાઈ
……………………. થાય. (2009)
(A) 393.4 nm
(B) 885.0 nm
(C) 442.5 nm
(D) 776.8 nm
જવાબ
(C) 442.5 nm
ધારો કે λ1 તરંગલંબાઈવાળા પ્રકાશમાંથી ‘n1‘ મી અને λ2 તરંગલંબાઈવાળા પ્રકાશથી ‘n2’ મી પ્રકાશિત શલાકા એકબીજા પર સંપાત થાય છે.

= 442.5 × 10-9m
= 442.5 nm
પ્રશ્ન 183.
ચંગના ડબલ સ્લિટ પ્રયોગમાં પડદા પરનાં P અને Q બિંદુઓએ સ્લિટો S1 અને S2 થી આવતા તરંગો સંપાત થાય છે. આ બિંદુઓ આગળ બંને તરંગો વચ્ચેનો પથતફાવત અનુક્રમે 0 અને
(A) 3 : 2
(B) 2 : 1
(C) √2 : 1
(D) 4 : 1
જવાબ
(B) 2 : 1

પ્રશ્ન 184.
યંગના એક પ્રયોગમાં પહેલા સુસંબદ્ધ અને ત્યારબાદ અસુસંબદ્ધ ઉદ્ગમોનો ઉપયોગ
કરવામાં આવે છે. જો પડદા પરના મધ્યસ્થ બિંદુએ મળતી તીવ્રતાઓ અનુક્રમે I1 અને I2 હોય, તો
(A) 4
(B) 2
(C) 1
(D) 0.5
જવાબ (B) 2
સુસંબદ્ધ ઉદ્ગમ માટે,

= I0cos2(0)
I1 = I0
પણ I0 = 4I’ મહત્તમ તીવ્રતા અને I’ = I1 કે I2 એક ઉદ્ગમની તીવ્રતા છે.
અસુસંબદ્ધ ઉદ્ગમ માટે,
I2 = I’ + I’ + 2
= 21′ + 2I’ (0) [∵ એક આવર્તકાળ પર < cosδ > = 0]
I2 = 2′
∴
∴
પ્રશ્ન 185.
યંગના એક પ્રયોગમાં એક સ્લિટ પહોળી છે, જ્યારે બીજી સ્લિટ સાંકડી છે. પહોળી
સ્લિટમાંથી આવતા પ્રકાશના તરંગો માટે કંપવિસ્તાર, બીજી સ્લિટમાંથી આવતા
પ્રકાશના તંરગોના કંપવિસ્તાર કરતાં બમણો છે. હવે જે સંપાતબિંદુએ સંપાત થતા
તરંગો વચ્ચેનો કળાતફાવત Φ હોય તો તે બિંદુએ પ્રકાશની તીવ્રતા I, મહત્તમ
તીવ્રતા Im ના પદમાં ……………………. થાય. (2012)
(A)
(A)
(C)
(D)
જવાબ
(D)
I ∝ A2
∴
અને સહાયક વ્યતિકરણ માટે પ્રકાશની મહત્તમ તીવ્રતા
Imax = Im = (A1 + A2)2 ચલનના અચળાંકનું મૂલ્ય 1 લેતાં
∴ Im = (2A2 + A2)2 [૨કમ પ્રમાણે A1 = 2A2]
∴ Im = (3A2)2
∴ Im = 9A22 ……………. (1)
પણ I2 ∝ A22
I2 = A22 [ચલનનો અચળાંક 1 લેતાં]
Im = 9I2 પરિણામ (1) પરથી
I2 =
હવે, બંને તરંગોની આપેલા બિંદુએ પ્રકાશની તીવ્રતા
I = I1 + I2 + 2
= 4I2 + I2 + 2
= 5I2 + 4I2ncosΦ
= I2 [1 + 4 + 4cosΦ]
= I2 [1 + 4 (1 + cosΦ)]
=
=
પ્રશ્ન 186.
I0 તીવ્રતા ધરાવતા અધ્રુવીભૂત પ્રકાશના બીમને પોલેરોઇડ A અને
ત્યારબાદ બીજા પોલેરોઇડ B માંથી પસાર કરવામાં આવે છે. પોલેરોઇડ B નું મુખ્ય
સમતલ પોલેરોઇડ A ની સાપેક્ષે 45° નો કોણ બનાવતું હોય, તો નિર્ગમન પામતા
પ્રકાશની તીવ્રતા …………………….. થશે. (2013)
(A)
(B) I0
(C)
(D)
જવાબ
(D)
માલસના નિયમ પરથી, A પોલેરોઇડમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા I1 = I0cos2θ
I1 =
B પોલેરાઇડમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I2 = I1cos2θ
=
=
પ્રશ્ન 187.
આકૃતિમાં દર્શાવ્યા પ્રમાણે બે સુસમ્બદ્ધ ઉદ્ગમો S1 અને S2 ખૂબ નાના અંતર ‘d’ થી અલગ કરેલા છે. પડદા પર મળતી શલાકાઓ ……………………. હશે. (2013)

(A) સમકેન્દ્રીય વર્તુળો
(B) બિંદુઓ
(C) સુરેખ રેખાઓ
(D) અર્ધવર્તુળો
જવાબ
(A) સમકેન્દ્રીય વર્તુળો

આકૃતિમાં દર્શાવ્યા અનુસાર શલાકાઓ પડદા ૫૨, સમકેન્દ્રીય વર્તુળો સ્વરૂપે મળે.
પડદા પર જેમનાં શિરોબિંદુઓ S1 અને S2 હોય તેવા બે શંકુઓ મળે કે જેમના પાયાઓ વર્તુળાકાર વલયો હોય.
પ્રશ્ન 188.
પરસ્પર લંબ સમતલમાં તલઘુવીભૂત કિરણપુંજનું A અને B પોલેરોઇડ વડે અવલોકન
કરવામાં આવે છે. જ્યારે કિરણપૂંજ A મહત્તમ તીવ્રતા અને કિરણપુંજ B શૂન્ય
તીવ્રતા ધરાવતું હોય તે સ્થિતિમાંથી પોલેરોઇડને 30° ના કોણે ભ્રમણ કરાવતા
બંને કિરણપુંજો સમાન તીવ્રતાથી દેખાય છે. જો બંને કિરણપુંજોની પ્રારંભિક
તીવ્રતા અનુક્રમે IA અને IB હોય, તો
(A)
(B) 1
(C)
(D) 3
જવાબ
(C)
ધારો કે કિરણપુંજ A ની મહત્તમ તીવ્રતા IA અને B કિરણપુંજની મહત્તમ તીવ્રતા IB છે.
B પોલેરોઇડને 30°નું ભ્રમણ આપતાં બંને કિરણપુંજોની તીવ્રતા સમાન છે.
∴ IAcos230° = IBcos260°

પ્રશ્ન 189.
એક પીન હોલના કેમેરાના બૉક્સની લંબાઈ L તથા તેમાં છિદ્રની ત્રિજ્યા ત છે.
એમ ધારવામાં આવે છે કે જો ી તરંગલંબાઈના સમાંતર ધારાવાળા પ્રકાશથી આ
છિદ્રને પ્રકાશિત કરવામાં આવે તો સ્પોટનો વિસ્તાર (કેમેરાની સામેની દીવાલ
પર મળતા) તેના ભૌમિતિક વિસ્તાર અને વિવર્તનના લીધેના વિસ્તારના સરવાળા
જેટલો હોય. આ સ્પોટની લઘુત્તમ સાઈઝ (bmin કરો) ત્યારે મળે કે જ્યારે (JEE – 2016)


જવાબ

પ્રશ્ન 190.
યંગના બે લિટના પ્રયોગમાં, સ્લિટો વચ્ચેનું અંતર 0.5 mm છે અને સ્ક્રીનને
150 cm દૂર રાખેલ છે. 650 nm અને 520 nm એમ બે તરંગલંબાઈ ધરાવતો પ્રકાશ
પુંજ પડદા પર વ્યતિકરણ મેળવવા માટે ઉપયોગમાં લેવાય છે. કોમન સેન્ટ્રલ
મહત્તમથી જ્યાં બંને તરંગલંબાઈઓ દ્વારા રચાતી તેજસ્વી શલાકાઓ સંપાત થાય છે
તેનું લઘુતમ અંતર છે. (JEE – 2017)
(A) 9.75 mm
(B) 15.6 mm
(C) 1.56mm
(D) 7.8mm
જવાબ
(D) 7.8mm

= 780000 × 10-6 cm
= 7.8mm
પ્રશ્ન 191.
એક નિરીક્ષક પ્રકાશની ગતિ કરતાં અડધી ગતિથી, 10 GHz આવૃત્તિના તરંગો
ઉત્પન્ન કરતાં એક સ્થિર માઇક્રોવેવ (microwave) ઉદ્ગમ તરફ જાય છે. આ
નિરીક્ષક દ્વારા મપાતી માઇક્રોવેવની આવૃત્તિનું મૂલ્ય હશે. (પ્રકાશની ગતિ =
3 × 108 ms-1)
(A) 17.3 GHz
(B) 15.3 GHz
(C) 10.1 GHz
(D) 12.1 GHz
જવાબ
(A) 17.3 GHz

= 10 × √3
= 10 × 1.73
= 17.3 GHz
પ્રશ્ન 192.
I તીવ્રતા ધરાવતો અધુવીભૂત પ્રકાશ એક આદર્શ પોલેરાઇઝર A માંથી પસાર થાય છે.
બીજો સમાન પોલેરાઇઝર B એ A ની પાછળ મૂકવામાં આવે છે. B ની આગળ/પછી
પ્રકાશની
તીવ્રતા
(A) 0°
(B) 30°
(C) 45°
(D) 60°
જવાબ
(D) 60°

અને આ કાર
A-પ્લેટમાંથી બહાર આવતાં પ્રકાશની તીવ્રતા
∴ C માંથી બહાર નીકળતાં પ્રકાશની તીવ્રતા
∴
∴
∴
∴ θ = 60°
પ્રશ્ન 193.
એક, એક સ્લિટ વિવર્તનભાતમાં મધ્યસ્થ મહત્તમની કોણીય જાડાઈ (પહોળાઈ) 60°
માલૂમ પડે છે. સ્લિટની પહોળાઈ 1um છે. સ્લિટ એકરંગી સમતલ તરંગો વડે
પ્રકાશિત કરવામાં આવે છે. હવે જો બીજી સમાન પહોળાઈ ધરાવતી સ્લિટ તેની નજીક
મૂકતા, સ્લિટથી 50 cm દૂર મૂકેલા પડદા ઉપર યંગની શલાકાઓ જોવા મળે છે. જો
અવલોકનમાં લીધેલ શલાકાની પહોળાઈ 1 cm હોય તો સ્લિટ વચ્ચેનું અંતર કેટલું
હશે ?
(એટલે કે દરેક લિટના કેન્દ્રથી તેમની વચ્ચેનું અંતર) (JEE – 2018)
(B) 50 μm
(A) 25 μm
(C) 75 μm
(D) 100 μm
જવાબ
(A) 25 μm
2θ = 60°
∴ θ = 30°
પ્રથમ ક્રમની ન્યૂનતમ શલાકા માટે,
∴ d sinθ = λ
d sin30° = λ
∴ d ×
λ =

= 25 × 10-6 m
∴ d’ = 25 μm
પ્રશ્ન 194.
આકૃતિમાં દર્શાવ્યા પ્રમાણેનો યંગનો બે લિટનો પ્રયોગ વિચારો. સ્લિટની સામે
સીધું જ પ્રથમ ન્યૂનતમ મળે તે માટે બે સ્લિટ વચ્ચેના અંતર d ને તરંગલંબાઈના
પદમાં કેટલું હોય ? JEE (Main)Jan – 2019)
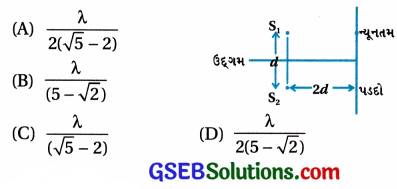
જવાબ

પ્રશ્ન 195.
એક પોલેરાઇઝર અને એનેલાઇઝર એવી રીતે ગોઠવેલ છે કે જેથી એનેલાઇઝરમાં બહાર
આવતાં પ્રકાશની તીવ્રતા, મૂળ તીવ્રતાના 10% હોય. એનેલાઇઝરને કેટલા કોણે
ફેરવવો જોઈએ કે જેથી તેમાંથી બહાર આવતાં પ્રકાશની તીવ્રતા શૂન્ય મળે ?
(ધારી લો કે પોલેરાઇઝર અને એનેલાઇઝરમાં કોઈ પ્રકાશ શોષાતો નથી.) (JEE Jan.-
2020)
(A) 60°
(B) 45°
(C) 18.4°
(D) 71.6°
જવાબ
(C) 18.4°
માલસના નિયમ પરથી,
I = I0cos2θ
0.1 I0 = I0cos2θ [∵ I = I0ના 10%]
∴ cos2θ = 0.1
∴ cosθ =
∴ cosθ = 0.3162
∴ θ = 71.6°
પરિભ્રમણ કરાવવો પડતો ખૂણો
= 90° – θ
= 90° – 71.6°
= 18.4°
પ્રશ્ન 196.
6000 × 10-8 cm તરંગલંબાઈવાળો દશ્યપ્રકાશ એક લિટ પર લંબરૂપે
આપાત થઈ વિવર્તન ભાત ઉત્પન્ન કરે છે. મધ્યમાન અધિકતમથી 60° ના કોણે બીજા
ક્રમનું ન્યૂનતમ મળે છે. જો પ્રથમ ન્યૂનતમ θ કોણે મળે તો 6નું નજીકનું
મૂલ્ય ……………………….. (JEE Jan.- 2020)
(A) 20°
(B) 25°
(C) 30°
(D) 45°
જવાબ
(B) 25°
બીજા ક્રમના ન્યૂનતમ માટે,
dsin θ = 2λ
∴ sinθ =
∴ sin 60° =
∴
∴
પ્રથમ ક્રમના ન્યૂનતમ માટે,
dsin θ = λ
∴ sinθ =
સમી. (1) પરથી
∴ sin θ =
sin θ = 0.4330
Sine ના ટેબલ પરથી
θ = 25.65°
∴ θ ≈ 25° (નજીકનું મૂલ્ય)
પ્રશ્ન 197.
YDSE (ચંગના ડબલ સ્લિટના પ્રયોગમાં) સ્લિટો વચ્ચેનું અંતર 0.15 mm છે.
સ્લિટો તથા પડદા વચ્ચેનું અંતર 1.5 m છે તથા પ્રકાશની તરંગલંબાઈ 589 nm છે,
તો શલાકાની પહોળાઈ ………………….. હશે. (JEE Jan.- 2020)
(A) 5.9 mm
(B) 3.9 mm
(C) 1.9 mm
(D) 2.3 mm
જવાબ
(A) 5.9 mm
શલાકાની પહોળાઈ
=
= 589 × 10-5 m
= 5.89 × 10-3 m
≈ 5.9 mm
પ્રશ્ન 198.
ઘણા મોટા આડછેદના ક્ષેત્રફળવાળા તલધ્રુવીભૂત પ્રકાશના બીમ (કિરણ)ની નિયમિત તીવ્રતા 3.3Wm-2 છે જે એક પૉલેરાઇઝર પર લંબરૂપે આપાત થાય છે (આડછેદનું ક્ષેત્રફળ 3 × 10-4m2).
આ પૉલેરાઇઝર તેના અક્ષને અનુલક્ષીને 31.4 rad/s ની કોણીય ઝડપથી ભ્રમણ કરે
છે, તો દર પરિભ્રમણ દીઠ પૉલેરાઇઝરમાંથી આશરે કેટલી ઊર્જા પસાર થશે ? (JEE
Main – 2020)
(A) 4.95 × 10-4
(B) 3.95 × 10-4
(C) 2.95 × 10-4
(D) 6.95 × 10-4
જવાબ
(A) 4.95 × 10-4
પ્રકાશની તીવ્રતા I =
E = IA
શરૂઆતમાં ઊર્જા = 0

= 4.95 × 10-4 J
પ્રશ્ન 199.
એક બસનો ડ્રાઇવર મોટી દીવાલ તરફ ગતિ કરતાં મોટી દીવાલ પાસેથી પરાવર્તિત
બસના હોર્નની આવૃત્તિમાં 420 Hz થી 490 Hz ફેરફાર અનુભવે છે. જો ધ્વનિની
ઝડપ 350 ms-1 હોય, તો બસની ઝડપ શોધો. (JEE Main – 2020)
(A) 81 km h-1
(B) 71 km h-1
(C) 61 km h-1
(D) 91 km h-1
જવાબ
(D) 91 km-1
ડ્રાઇવરને સંભળાતી આવૃત્તિ f’ = 490 Hz
બસના હૉર્નની ધ્વનિની આવૃત્તિ f = 420 Hz
બસની ઝડપ = vs, ધ્વનિની ઝડપ = v
ડ્રાઇવરને સંભળાતા ધ્વનિની આવૃત્તિ,

= 91.37 km h-1
≈ 91 km h-1
પ્રશ્ન 200.
0.6 × 10-4 m જાડાઈની એક લિટને 6000 × 10-10 m
તરંગલંબાઈના નારંગી પ્રકાશથી પ્રકાશિત કરેલી છે. વિવર્તનમાં મધ્યસ્થ
અધિકતમની બંને બાજુએ ન્યૂનતમની સંખ્યા કેટલી મળે ? (JEE Main – 2020)
જવાબ
વિવર્તનમાં ન્યૂનતમની શરત,
dsinθ = nλ
∴ sinθ =
પણ sinθ નો મહત્તમ વિસ્તાર 1
∴ sinθ ≤ 1
∴ 1 ≥
∴
∴
∴ 100 ≥ n
∴ મધ્યસ્થ અધિકતમની એક બાજુએ ન્યૂનતમની સંખ્યા = 100
∴ મધ્યસ્થ અધિકતમની બંને બાજુએ ન્યૂનતમની સંખ્યા = 100 + 100 = 200
પ્રશ્ન 201.
જો બે સુસમ્બદ્ધ ઉદ્ગમોના પ્રકાશની તીવ્રતાનો ગુણોત્તર 2x હોય, તો
(A)
(B)
(C)
(D)
જવાબ
(A)

પ્રશ્ન 202.
વિધાન : ઇલેક્ટ્રોન માઇક્રોસ્કોપની વિભેદન શક્તિ, પ્રકાશીય માઇક્રોસ્કોપની વિભેદન શક્તિ કરતાં મોટી હોય છે.
કારણ : દૃશ્ય પ્રકાશના તરંગની તરંગલંબાઈ કરતાં ઇલેક્ટ્રૉનની તરંગલંબાઈ મોટી છે. (JEE Main Feb. – 2021)
(A) વિધાન સાચું, કારણ સાચું પણ કારણ એ વિધાનની સાચી સમજૂતી નથી.
(B) વિધાન સાચું, કારણ સાચું અને કારણ એ વિધાનની સાચી સમજૂતી છે.
(C) વિધાન સાચું અને કારણ ખોટું
(D) વિધાન ખોટું અને કારણ સાચું
જવાબ
(B) વિધાન સાચું, કારણ સાચું અને કારણ એ વિધાનની સાચી સમજૂતી છે.
ઇલેક્ટ્રૉનની તરંગલંબાઈ, દશ્ય પ્રકાશની તરંગલંબાઈ કરતાં ઓછી હોય છે. તેથી
ઇલેક્ટ્રૉન માઇક્રોસ્કોપની વિભેદન શક્તિ, પ્રકાશીય માઇક્રોસ્કોપની વિભેદન
શક્તિ કરતાં વધારે હોય છે.
પ્રશ્ન 203.
YDSE પ્રયોગમાં સ્લિટો અને પડદા વચ્ચેનું અંતર 1 m અને બે લિટો વચ્ચેનું
અંતર 2mm તથા પ્રકાશની તરંગલંબાઈ 500 nm છે, તો શલાકાની પહોળાઈ ……………………
(JEE Main Feb. – 2021)
(A) 0.25 mm
(B) 0.2 mm
(C) 0.30 mm
(D) 0.40 mm
જવાબ
(A) 0.25 mm
શલાકાની પહોળાઈ,
β =
β = 0.25 mm
પ્રશ્ન 204.
નીચેનામાંથી કઈ ઘટના પ્રકાશ અને ધ્વનિ માટે સામાન્ય નથી ? (1988)
(A) વ્યતિકરણ
(B) વિવર્તન
(C) વક્રીભવન
(D) ધ્રુવીભવન
જવાબ
(D) ધ્રુવીભવન
પ્રશ્ન 205.
વ્યતિકરણ શેમાં શક્ય છે ? (1989)
(A) માત્ર પ્રકાશના તરંગોમાં
(B) માત્ર ધ્વનિના તરંગોમાં
(C) ધ્વનિ અને પ્રકાશ બંનેનાં તરંગોમાં
(D) ધ્વનિ અને પ્રકાશ બંનેમાંથી એક પણ નહિ.
જવાબ
(C) ધ્વનિ અને પ્રકાશ બંનેનાં તરંગોમાં
પ્રશ્ન 206.
4360Å અને 5460Å તરંગલંબાઈવાળા વાદળી અને લીલા રંગના પ્રકાશ માટે યંગનો
પ્રયોગ કરવામાં આવે છે. જો ચોથી પ્રકાશિત શલાકાનું અંતર x હોય તો, (1990)
(A) x (વાદળી) = x (લીલો)
(B) x (વાદળી) > x (લીલો)
(C) x (વાદળી) < x (લીલો)
(D) 
જવાબ
(C) x (વાદળી) < x (લીલો)
n મા અધિકતમનું અંતર x = nλ
∴ x ∝ λ
∴ λવાદળી < λલીલો ∴ x(વાદળી) < x(લીલો)
પ્રશ્ન 207.
રંગના પ્રયોગમાં શલાકાની પહોળાઈ 0.4mm છે. હવે જો આ સમગ્ર રચનાને
આવે તો શલાકાની પહોળાઈ કેટલી થશે ? (1990)
(A) 0.3 mm
(B) 0.4 mm
(C) 0.53 mm
(D) 450 um
જવાબ
(A) 0.3 mm
β’ =
પ્રશ્ન 208.
બે તરંગોની તીવ્રતાઓનો ગુણોત્તર 4 : 1 છે, તો તેમના કંપવિસ્તારોનો ગુણોત્તર કેટલો થશે ? (1991)
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
જવાબ
(A) 2 : 1
∴
પ્રશ્ન 209.
નીચેનામાંથી કઈ ઘટના હાઇગેન્સના તરંગ-અગ્ર માટેના સિદ્ધાંત પરથી સમજાવી શકાતી નથી ? (1992-1988)
(A) વક્રીભવન
(B) પરાવર્તન
(C) વિવર્તન
(D) વર્ણપટ
જવાબ
(D) વર્ણપટ
પ્રશ્ન 210.
રંગના વ્યતિકરણના પ્રયોગમાં એકબીજાથી 0.9mm અંતરે રહેલા બે સુસમ્બદ્ધ
ઉદ્ગમો વડે મળતી શલાકા 1m દૂર મળે છે. જો બીજી અપ્રકાશિત શલાકા મધ્યસ્થ
પ્રકાશિત શલાકાથી 1mm દૂર હોય તો ઉપયોગમાં લીધેલ એકરંગી પ્રકાશની તરંગલંબાઈ
કેટલી હશે ? (1991-1992)
(A) 60 × 10-4 cm
(B) 10 × 10-4 cm
(C) 10 × 10-5 cm
(D) 6 × 10-5 cm
જવાબ
(D) 6 × 10-5 cm
અપ્રકાશિત શલાકા માટે,
x = (2n – 1)
∴ λ =
λ = 0.6 × 10-6 m
∴ = 6 × 10-5 cm
પ્રશ્ન 211.
યંગના વ્યતિકરણના પ્રયોગમાં ઉપયોગમાં લેવાયેલ પ્રકાશની તરંગલંબાઈ 5000Å છે.
બે સ્લિટ વચ્ચેનું અંતર 0.2 mm છે. સ્લિટ અને પડદા વચ્ચેનું અંતર 200 cm
છે. જો મધ્યસ્થ શલાકા x = 0 પાસે હોય તો ત્રીજી પ્રકાશિત શલાકા માટે x =
………………….. (1992)
(A) 1.67 cm
(B) 1.5 cm
(C) 0.5 cm
(D) 5.0 cm
જવાબ
(B) 1.5 cm
x = (n) λ
= 3 × 5000 × 10-10 ×
= 1.5 × 10-2 m = 1.5 cm
પ્રશ્ન 212.
જો યંગના વ્યતિકરણના પ્રયોગમાં એકરંગી વાદળી પ્રકાશને સ્થાને તેટલી જ
તીવ્રતાવાળો સોડિયમ લેમ્પ દ્વારા મળતો પીળો પ્રકાશ લેવામાં આવે તો ……………………
(1992)
(A) શલાકાની પહોળાઈ ઘટશે.
(B) શલાકાની પહોળાઈ વધશે
(C) શલાકાની પહોળાઈ તેની તે જ રહેશે.
(D) શલાકાની તીવ્રતા ઘટશે.
જવાબ
(A) શલાકાની પહોળાઈ ઘટશે.
∴
∴
∴ શલાકાની પહોળાઈ ઘટશે.
પ્રશ્ન 213.
વ્યતિકરણ ઘટનામાં હવા હાજર હોય તેવા તંત્રમાં અવલોકન કરવામાં આવે છે. હવે
જો તંત્રમાં શૂન્યાવકાશ કરવામાં આવે અને તે જ પ્રકાશનો ઉપયોગ કરવામાં આવે
તો શું અવલોકન મળશે ? (1993)
(A) વ્યતિકરણ નહીં મળે.
(B) ઘાટી પ્રકાશિત શલાકાઓ સાથે વ્યતિકરણ મળશે.
(C) આછી પ્રકાશિત શલાકાઓ સાથે વ્યતિકરણ મળશે.
(D) પહોળી પ્રકાશિત શલાકાઓ સાથે વ્યતિકરણ મળશે.
જવાબ
(D) પહોળી પ્રકાશિત શલાકાઓ સાથે વ્યતિકરણ મળશે.
પ્રશ્ન 214.
0.001 mm ની પહોળાઈ ધરાવતી એક સાંકડી સ્લિટ પર 5000 Å તરંગલંબાઈ ધરાવતા
એકરંગી પ્રકાશનું સમાંતર બીમ (Beam) આપાત કરવામાં આવે છે. હવે આ પ્રકાશને
એક બહિર્ગોળ લેન્સના ફોકલ પ્લેન પર રાખેલા પડદા પર કેન્દ્રીત કરવામાં આવે
છે, તો આ વ્યતિકરણ માટે પ્રથમ ન્યૂનતમ કેટલા ખૂણે મળશે ? (1993)
(A) 0°
(B) 15°
(C) 30°
(D) 50°
જવાબ
(C) 30°
પ્રથમ ન્યૂનતમ માટે dsinθ = nλ = 1λ [∵ n = 1]
sinθ =
∴ θ = 30°
પ્રશ્ન 215.
ફ્રેનલના biprism ના પ્રયોગમાં લેન્સની બે જુદી જુદી સ્થિતિઓ માટે સ્લિટો
વચ્ચેનું અંતર 16 cm અને 9 cm મળે છે, તો તેમના વચ્ચેનું સાચું અંતર કેટલું
હશે ?(1996)
(A) 12.5 cm
(B) 12 cm
(C) 13 cm
(D) 14cm
જવાબ
(B) 12 cm
સાચું અંતર
પ્રશ્ન 216.
સાબુ વડે મળતી પાતળી પોટી અને સાબુના પરપોટા પર જોવા મળતા રંગ …………………. પર આભારી છે. (1999)
(A) વક્રીભવન
(B) વિભાજન
(C) વ્યતિકરણ
(D) વિવર્તન
જવાબ
(C) વ્યતિકરણ
પ્રશ્ન 217.
એક કાગળ પર બે બિંદુઓ વચ્ચેનું અંતર તું છે. તે અવલોકનકારની દૃષ્ટિરેખા
તેને લંબરૂપે રહે તે રીતે અવલોકન કરે છે. અવલોકનકારની આંખના લેન્સનો વ્યાસ
2mm છે. d ના કયા લઘુતમ મૂલ્ય માટે બે બિંદુઓને એકબીજાથી જુદા જોઈ શકાશે ?
પ્રકાશની તરંગલંબાઈ 5000Å લો. (2002)
(A) 1.25 m
(B) 12.5 cm
(C) 1.25 cm
(D) 2.5 mm
જવાબ
(B) 12.5 cm
આંખની વિભેદનશકિત θ =
જયાં d = આંખના લેન્સનો વ્યાસ
બે બિંદુઓ વચ્ચેનું અંતરY અને આંખથી અંતર D હોય તો θ =
Y =
પ્રશ્ન 218.
રંગના બે લિટના પ્રયોગમાં જો બે સ્લિટ વચ્ચેનું અંતર ઘટાડીને
(A) 3
(B)
(C) 9
(D)
જવાબ
(A) 3
શલાકાની પહોળાઈ β =

પ્રશ્ન 219.
I1 અને I2 તીવ્રતાવાળા પ્રકાશના તરંગો કોઈ એક
વિસ્તારમાંથી સરખા સમયમાં એક જ દિશામાં પસાર થાય છે, તો તેની મહત્તમ અને
ન્યૂનતમ તીવ્રતાનો સરવાળો કેટલો થશે ?’ (CBSE PMT – 2008)
(A) I1 + I2
(B) (
(C) (
(D) 2I1 + I2)
જવાબ
(D) 2I1 + I2)
પરિણામી તીવ્રતા I = I1 + I2 + 2
મહત્તમ તીવ્રતા માટે cos Φ = 1
Imax = I1 + I2 + 2
ન્યૂનતમ તીવ્રતા માટે cos Φ = -1
Imin = I1 + I2 – 2
હવે, Imax + Imin
= I1 + I2 + 2
= 2(I1 + I2)
પ્રશ્ન 220.
યંગના બે સ્લિટના પ્રયોગમાં બે સ્લિટો વચ્ચેનું અંતર 2 mm છે. તેમને λ1 = 12000 Å અને λ2
= 10000 Å ના ફોટોનથી પ્રકાશિત કરેલ છે. તો મધ્યસ્થ પ્રકાશિત શલાકાના
મધ્યબિંદુથી કેટલા લઘુતમ અંતરે બંને તરંગલંબાઈઓથી મળતી પ્રકાશિત શલાકાઓ
સંપાત થશે ? લિટથી પડદાનું અંતર 2 m છે. (NEET 2013)
(A) 4 mm
(B) 3 m
(C) 8 mm
(D) 6 mm
જવાબ
(D) 6 mm
ધારો કે λ1 તરંગલંબાઈની n1 મી અને λ2 તરંગલંબાઈની n2 મી પ્રકાશિત શલાકાઓ સંપાત થાય છે.

પ્રશ્ન 221.
ઝડપી ગતિ કરતા ઇલેક્ટ્રોનનું સમાંતર કિરણજૂથ સાંકડી સ્લિટ પર લંબરૂપે આપાત
થાય છે. પડદાથી ઘણે દૂર એક પ્રસ્ફુરક પડદો મૂકેલો છે. જો ઇલેક્ટ્રૉનની ઝડપ
વધારવામાં આવે તો નીચેનામાંથી કયું વિધાન સાચું છે ?(NEET 2013)
(A) મધ્યસ્થ અધિકતમની કોણીય પહોળાઈ ઘટશે.
(B) મધ્યસ્થ અધિકતમની કોણીય પહોળાઈ ૫૨ અસર થશે નહીં.
(C) ઈલેક્ટ્રૉનના કિસ્સામાં વિવર્તનભાત દેખાશે નહીં.
(D) મધ્યસ્થ અધિકતમની કોણીય પહોળાઈ વધશે.
જવાબ
(A) મધ્યસ્થ અધિકતમની કોણીય પહોળાઈ ઘટશે.
ઇલેક્ટ્રૉનની તરંગ લંબાઈ λ =
∴ λ ∝
તેથી ઝડપ વધતાં λ ઘટે અને વિવર્તનનો અધાર sinθ ∝ λ હોવાથી λ ઘટતાં sinθ ઘટે તેથી θ ઘટે પરિણામે કોણીય પહોળાઈ ઘટે.
પ્રશ્ન 222.
દૂર રહેલા કોઈ ઉદ્ગમમાંથી λ = 600 nm તરંગલંબાઈના પ્રકાશનું કિરણજૂથ 1mm
પહોળાઈની સ્લિટ પર આપાત થાય છે. તેથી મળતી વિવર્તન ભાત, સ્લિટથી દૂર
રાખેલાં પડદા પર મળે છે, તો મધ્યમાન પ્રકાશિત શલાકાની બંને બાજુની પ્રથમ
અપ્રકાશિત શલાકા વચ્ચેનું અંતર ………………… હશે. (NEET 2014)
(A) 1.2 cm
(B) 1.2 mm
(C) 2.4 cm
(D) 2.4mm
જવાબ
(D) 2.4mm
પ્રથમ ન્યૂનતમ માટેની શરત,
dsinθ1 = λ
∴ sinθ1 =
પણ sinθ1 =
∴
∴ x1 =
∴ મધ્યસ્થ અધિકતમની બંને બાજુના પ્રથમ ન્યૂનતમ વચ્ચેનું અંતર = 2x1
∴ 2x1 =
=
= 2400 × 10-6 m
= 2.4 mm
પ્રશ્ન 223.
યંગના બે લિટના પ્રયોગમાં જ્યાં પથ-તફાવત λ છે તે બિંદુએ પ્રકાશની તીવ્રતા મળે છે, તો જે બિંદુએ પથ-તફાવત
(A) k
(B)
(C)
(D) શૂન્ય
જવાબ
(C)

પ્રશ્ન 224.
જો વસ્તુકાચની કેન્દ્રલંબાઈ વધારવામાં આવે તો વિવર્ધનશક્તિ …………………… (NEET 2014)
(A) માઇક્રોસ્કોપની વધશે પણ ટેલિસ્કોપની ઘટશે.
(B) માઇક્રોસ્કોપ અને ટેલિસ્કોપ બંનેની વધશે.
(C) માઇક્રોસ્કોપ અને ટેલિસ્કોપ બંનેની ઘટશે.
(D) માઇક્રોસ્કોપની ઘટશે પણ ટેલિસ્કોપની વધશે.
જવાબ
(D) માઇક્રોસ્કોપની ઘટશે પણ ટેલિસ્કોપની વધશે.
માઇક્રોસ્કોપની વિવર્ધનશક્તિ =
∴ f0 વધારતાં તેની વિવર્ધનશક્તિ ઘટે.
જ્યારે, ટેલિસ્કોપની વિવર્ધનશક્તિ =
∴ f0 વધારતાં તેની વિવર્ધનશક્તિ વધે.
પ્રશ્ન 225.
એકરંગી સમાંતર કિરણ જૂથની તરંગલંબાઈ λ છે. જ્યારે લિટની પહોળાઈ એ પ્રકાશની
તંરગલંબાઈના ક્રમની હોય ત્યારે વિવર્તન રચાય છે. જો સ્લિટ અને પડદા
વચ્ચેનું અંતર D હોય તો મધ્યસ્થ અધિકતમની પહોળાઈ કેટલી ? (NEET May 2015)
(A)
(B)
(C)
(D)
જવાબ
(A)
મધ્યસ્થ અધિકતમની રેખીય પહોળાઈ એટલે પડદા પરના બે પ્રથમ ન્યૂનતમો વચ્ચેનું અંતર
∴ પ્રથમ ન્યૂનતમ માટેની શરત,
dsinθ = nλ માં d = a, n = 1
∴ sinθ =
∴ મધ્યસ્થ અધિકતમની રેખીય પહોળાઈ = D[2θ]
=
પ્રશ્ન 226.
બે લિટના પ્રયોગમાં બે લિટો વચ્ચેનું અંતર 1 mm અને સ્વિટથી પડદા વચ્ચેનું
અંતર 1m છે. 500 nm તરંગલંબાઈ ધરાવતા એકરંગી પ્રકાશનો ઉપયોગ કર્યો છે. બે
સ્લિટ માટે દસમાં અધિકતમ જેટલું જ એક લિટથી મધ્યસ્થ અધિક્તમ મળે તો દરેક
લિટની પહોળાઈ કેટલી ? (NEET May 2015)
(A) 0.2 mm
(B) 0.1 mm
(C) 0.5 mm
(D) 0.02 mm
જવાબ
(A) 0.2 mm
બે સ્લિટના પ્રયોગમાં દસમાં અધિકતમનું કોણીય અંતર
dsinθ10 = 10λ
∴ sinθ10 =
હવે, એક સ્લિટની મદદથી મધ્યસ્થ અધિકતમની કોણીય પહોળાઈ
∴ sin2θ1 =
પણ sinθ10 = sin2θ1
∴ d’ = 0.2 mm [∵ d = 1 mm]
પ્રશ્ન 227.
એક સ્વિટથી થતા વિવર્તનમાં મધ્યસ્થ અધિકતમની નજીકની પ્રથમ ન્યૂનતમ પર,
લિટની ધાર (એક છેડે) તથા તેના મધ્યમાં રહેલા બિંદુમાંથી ઉત્પન્ન થતી
હાઇગેન્સ તરંગ- અગ્રોની વચ્ચેનો કળા-તફાવત કેટલો હશે ? (NEET July 2015)
(A)
(B)
(C)
(D) πrad
જવાબ
(D) πrad
કાટકોણ ΔS1 NS માં sinθ =
sinθ =
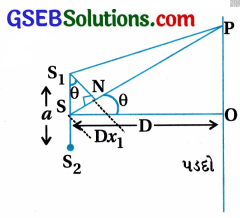
∴ Δx1 =
જ્યાં Δx1 એ પથ-તફાવત છે.
હવે, પ્રથમ ન્યૂનતમ માટે,
a sinθ = λ [∵ d = a છે]
∴ sinθ =
∴ Δx1 =
હવે, કળા-તફાવત ΔΦ1 = k ×પથ-તફાવત
=
=
= πrad
પ્રશ્ન 228.
યંગના બે સ્લિટના પ્રયોગમાં જો તેમની પહોળાઈનો ગુણોત્તર 1: 25 હોય તો
વ્યતિકરણથી મળતી મહત્તમ અને લઘુતમ તીવ્રતાનો ગુણોત્તર ………………….. . (GUJCET-
2007) (NEET July 2015)
(A)
(B)
(C)
(D)
જવાબ
(B)
ધારો કે સ્વિટની પહોળાઈ W1 અને W2 છે.
હવે, I ∝ W


પ્રશ્ન 229.
યંગના બે સ્લિટના પ્રયોગમાં મધ્યસ્થ અધિકતમની તીવ્રતા I0 છે.
બંને સ્લિટો વચ્ચેનું અંતર d = 5λ છે, જ્યાં λ એ પ્રયોગમાં વપરાયેલ
પ્રકાશની તરંગલંબાઈ છે. કોઈ એક લિટની સામે D = 10d અંતરે આવેલા પડદા પર
તીવ્રતા કેટલી હશે ? (NEET May 2016)
(A)
(B)
(C)
(D) I0
જવાબ
(C)

પ્રશ્ન 230.
એક સ્વિટની પહોળાઈ ‘a’ પર 5000 Å તરંગલંબાઈનો પ્રકાશ આપાત કરવામાં આવે
ત્યારે મળતા વિવર્તનમાં 30° ના ખૂણે પ્રથમ ન્યૂનતમ મળે છે, તો પ્રથમ મહત્તમ
કેટલા કોણે દેખાશે ? (NEET May 2016)
(A) sin-1(
(B) sin-1(
(C) sin-1(
(D) sin-1(
જવાબ
(C) sin-1(
પ્રથમ ન્યૂનતમ માટે
asinθ = λ [n = 1]·
∴ asin30° = λ
∴ a ×
∴ a = 2λ
પ્રથમ અધિકતમ માટે
asinθ1 = (2n + 1)
∴ asinθ1 =
∴ 2λsinθ1 =
∴ sinθ1 =
∴ θ1 = sin-1(
પ્રશ્ન 231.
બે સુસમ્બદ્ધ ઉદ્ગમોમાંથી ઉત્સર્જાતા પ્રકાશની તીવ્રતાનો ગુણોત્તર n છે. તેમના વડે રચાતી વ્યતિકરણ ભાત માટે
(A)
(B)
(C)
(D)
જવાબ
(D)
ધારો કે પ્રકાશની તીવ્રતાઓ I1 અને I2 છે.

ફરીથી વિયોગ-યોગ કરતાં,

પ્રશ્ન 232.
0.02 cm પહોળાઈની એક રેખીય સ્લિટને એક 60 cm કેન્દ્રલંબાઈવાળા લેન્સની નજીક સ્લિટની સામે રાખેલ છે. આ સ્વિટને 5 × 10-5
cm તરંગલંબાઈવાળા લંબરૂપે આપાત પ્રકાશના સમાંતર કિરણપુંજ વડે પ્રકાશિત
કરેલો છે, તો મળતી વિવર્તન ભાતમાં પ્રથમ અપ્રકાશિત શલાકાનું કેન્દ્રથી અંતર
કેટલું હશે ? (NEET July 2016)
(A) 0.20 cm
(B) 0.15 cm
(C) 0.10 cm
(D) 0.25 cm
જવાબ
(B) 0.15 cm
m માં ક્રમની અપ્રકાશિત શલાકા માટે,
-dsinθm mλ

= 0.15 cm
પ્રશ્ન 233.
જેમની તીવ્રતાનો ગુણોત્તર ૦ છે તેવા બે સુસમ્બદ્ધ ઉદ્ગમો અંતરક્ષેપ પામે છે.
(A) 2
(B)
(C)
(D)
જવાબ
(B)
પ્રશ્ન 234.
λ તરંગલંબાઈનો એક સમાંતર પ્રકાશ પુંજ d પહોળાઈની એક સિંગલ સ્લિટ પર લંબરૂપે
આપાત થાય છે. વિવર્તન ભાત એ લિટથી D અંતરે મૂકેલ પડદા પર મળે છે. મધ્ય
તેજસ્વી બૅન્ડથી કેટલા અંતરે દ્વિતીય અપ્રકાશિત બેન્ડ મળશે તે આપવામાં આવે
છે : (NEET 2017)
(A)
(B) λ d D
(C)
(D)
જવાબ
(A)
વિવર્તન માટે અપ્રકાશિત શલાકા માટેની શરત
dsinθn = nλ
પણ નાના ખૂણા માટે sinθn =
x2 =
પ્રશ્ન 235.
જેનો વક્રીભવનાંક ‘µ’ છે તેવા દ્રવ્યની સમતલ સપાટી હવામાંથી અવીભૂત પ્રકાશ
આપાત થાય છે. કોઈ ચોક્કસ આપાતકોણ ‘i’ પર એમ જોવા મળ્યું કે પરાવર્તિત અને
વક્રીભૂત કિરણો એકબીજાને લંબ છે. આ પરિસ્થિતિ માટે નીચેનાં વિધાનોમાંથી
કયું સાચું છે? (NEET 2018)
(A) i = tan-1(
(B) આપાત સમતલને તેનો વિદ્યુત સદિશ સમાંતર રહે તેમ પરાવર્તિત પ્રકાશ ધ્રુવીભૂત થાય છે.
(C) i = sin-1(
(D) આપાત સમતલને તેનો વિદ્યુત સદિશ લંબ રહે તેમ પરાવર્તિત પ્રકાશ ધ્રુવીભૂત થાય છે.
જવાબ
(D) આપાત સમતલને તેનો વિદ્યુત સદિશ લંબ રહે તેમ પરાવર્તિત પ્રકાશ ધ્રુવીભૂત થાય છે.
પરાવર્તનથી થતાં ધ્રુવીભવનમાં જ્યારે પરાવર્તિત કિરણ અને વક્રીભૂત કિરણ
પરસ્પર લંબ હોય તો પરાવર્તિત કિરણમાં થોડા σ ઘટકો (જે આપાત સમતલને લંબ હોય)
જ હોય છે.
પ્રશ્ન 236.
યંગના ડબલ-સ્લિટના પ્રયોગમાં સ્લિટ વચ્ચેનું અંતર d એ 2 mm, ઉપયોગમાં
લેવાનાં પ્રકાશની તરંગ લંબાઈ λ એ 5896 Å અને પડદા અને સ્લિટ વચ્ચેનું અંતર D
એ 100 cm છે. એમ જોવા મળ્યું કે શલાકાઓની કોણીય પહોળાઈ 0.20° છે. આ
શલાકાઓની કોણીય પહોળાઈ વધારીને 0.21° કરવા માટે (λ અને D બદલ્યા વગર) આ
લિટસ વચ્ચેનું અંતર રાખવું જરૂરી છે, (NEET 2018)
(A) 1.7 mm
(C) 2.1 mm
(B) 1.8mm
(D) 1.9 mm
જવાબ
(D) 1.9 mm
યંગના પ્રયોગમાં d sinθ1 = (b) λ માં જો θ નાનો હોય તો
sinθ1 = θ1
∴ dθ1 = λ
∴ θ1 =
∴ θ ∝
∴
∴
= 2 ×
= 1.9 mm
પ્રશ્ન 237.
કોઈ ખગોળીય વક્રીભૂત દૂરબીનને મોટું કોણીય વિવર્ધન અને ઉચ્ચ કોણીય વિભેદન હશે જ્યારે તેનો વસ્તુ કાચ, (NEET 2018)
(A) નાની કેન્દ્રલંબાઈ અને નાના વ્યાસનો હોય
(B) નાની કેન્દ્રલંબાઈ અને મોટા વ્યાસનો હોય
(C) મોટી કેન્દ્રલંબાઈ અને મોટા વ્યાસનો હોય
(D) મોટી કેન્દ્રલંબાઈ અને નાના વ્યાસનો હોય
જવાબ
(C) મોટી કેન્દ્રલંબાઈ અને મોટા વ્યાસનો હોય
ખગોળીય દૂરબીન મોટવણી =
વસ્તુ કાચની કેન્દ્રલંબાઈ (f0) મોટી અથવા આઇપીસની કેન્દ્રલંબાઈ નાની હોવી જોઈએ અને કોણીય વિભેદન
∴ કોણીય વિભેદન ∝ D
તેથી લેન્સનો વ્યાસ (D) મોટો રાખવાથી કોણીય વિભેદન મોટું મળે.
પ્રશ્ન 238.
બે-સ્લિટના પ્રયોગમાં જ્યારે 400 nm તરંગ લંબાઈનો પ્રકાશ વપરાય છે ત્યારે 1
m દૂર મૂકેલ પડદા પર રચાતી પ્રથમ ન્યૂનતમની કોણીય પહોળાઈ 0.2° જોવા મળી
હતી. જો આ આખા પ્રયોગના સાધનને પાણીમાં ડુબાડવામાં આવે તો આ પ્રથમ
ન્યૂનતમની કોણીય પહોળાઈ શું હશે ?
(μ પાણી = 4/3) (NEET – 2019)
(A) 0.1°
(B) 0.266°
(C) 0.15°
(D) 0.05°
જવાબ
(C) 0.15°

પ્રશ્ન 239.
એક આંતરપૃષ્ઠ માટે બ્રુસ્ટકોણ ib હોય છે. (NEET-2020)
(A) 0° < ib < 30°
(B) 30°< ib < 45°
(C) 45° < ib < 90°
(D) ib = 90°
જવાબ
(C) 45° < ib < 90°
બ્રેસ્ટરના નિયમ પરથી,
tanib = n
હંમેશાં n > 1
∴ tanib > 1
∴ ib > 45° [∵ 1 = tan45°]
∴ 45° < ib < 90°
પ્રશ્ન 240.
કોઈ એક તારામાંથી 600 nm તરંગલંબાઈનો પ્રકાશ આવે છે તેમ ધારો. 2m વ્યાસના
ઓબ્જેક્ટિવ ધરાવતાં ટેલિસ્કોપની વિભેદન સીમા ……………………… છે. (NEET-2020)
(A) 3.66 × 10-7 rad
(B) 1.83 × 10-7 rad
(C) 7.32 × 10-7 rad
(D) 6.00 × 10-7 rad
જવાબ
(A) 3.66 × 10-7 rad
વિભેદન સીમા λmin =
=
= 3.66 × 10-7 rad
પ્રશ્ન 241.
I અને 4I તીવ્રતાવાળા બે તરંગો સંપાત થાય ત્યારે મહત્તમ અને ન્યૂનતમ તીવ્રતાઓ અનુક્રમે ……………………. અને …………………. થશે. (1997)
(A) 5I, 3I
(B) 9I, I
(C) 9I, 3I
(D) 5I, I
જવાબ
(B) 9I, I
Imax = I1 + I2 + 2
= I + 4I + 2
= 5I + 2 × 2I = 9I
Imin = I1 + I2 + 2
= I + 4I + 2
= 5I – 4I = I
પ્રશ્ન 242.
જો ……………………. તો પ્રકાશ સીધી રેખામાં ગતિ કરતાં દેખાય. (1998)
(A) તે વાતાવરણમાં ન શોષાય
(B) તે વાતાવરણમાં પરાવર્તન પામે
(C) તેની તરંગલંબાઈ ઘણી જ નાની હોય
(D) તેનો વેગ ઘણો જ મોટો હોય
જવાબ
(C) તેની તરંગલંબાઈ ઘણી જ નાની હોય
વિવર્તન નહિવત્ થવાથી.
પ્રશ્ન 243.
………………….. માં વ્યતિકરણની ઘટના જોવા મળે છે. (1999)
(A) માત્ર સંગત યાંત્રિક તરંગો
(B) માત્ર લંબગત યાંત્રિક તરંગો
(C) માત્ર વિદ્યુતચુંબકીય તરંગો
(D) બધા જ પ્રકારના તરંગો
જવાબ
(D) બધા જ પ્રકારના તરંગો
પ્રશ્ન 244.
રંગના પ્રયોગમાં એક લિટની સામે 1.5 વક્રીભવનાંક અને 2.5 × 10-5 m
જાડાઈનું એક પારદર્શક માધ્યમ રાખવામાં આવેલું છે, તો વ્યતિકરણ શલાકાનું
કેટલું સ્થાનાંતર (શિફ્ટ) થશે ? (d = 0.5 mm અને D = 100 cm લો.) (1999)
(A) 5 cm
(B) 2.5 cm
(C) 0.25 cm
(D) 0.1 cm
જવાબ
(B) 2.5 cm
વ્યતિકરણ શલાકાનું સ્થાનાંતર Δx ધારો
હવે,
∴ Δx =
∴ Δx =
=
= 2.5 × 10-2 m = 2.5 cm
પ્રશ્ન 245.
વિનાશક઼ વ્યતિકરણ માટેનો પથ-તફાવત ………………….. છે. (2002)
(A) nλ
(B)
(C) n (λ + 1)
(D)
જવાબ
(D)
વિનાશક વ્યતિકરણ માટે પથ-તફાવતનું સૂત્ર,
પ્રશ્ન 246.
દરિયાઈ છીપમાં જોવા મળતો સોનેરી રંગ ……………………. ને કારણે હોય છે. (2002)
(A) વિવર્તન
(B) ધ્રુવીભવન
(C) પ્રકીર્ણન
(D)પરાવર્તન જવાબ
(B) ધ્રુવીભવન
જ્યારે દરિયાઈ છીપ પર પ્રકાશ પડે છે ત્યારે તેનો થોડોક ભાગ જે વક્રીભવન
પામે છે તે આંશિક ધ્રુવીભૂત થયેલો હોય છે અને ત્યારબાદ તે પૂર્ણ ધ્રુવીભૂત
પ્રકાશ તરીકે પરાવતર્ન પામતા છીપ સોનેરી રંગની જણાય છે.
પ્રશ્ન 247.
જ્યારે વસ્તુના સ્થાનને નક્કી કરવા પ્રકાશના કિરણજૂથનો ઉપયોગ થાય છે ત્યારે જો પ્રકાશ …………………… હોય તો મહત્તમ ચોકસાઈ મળે છે. (2003)
(A) ધ્રુવીભૂત
(B) લાંબી તરંગલંબાઈવાળો
(C) ટૂંકી તરંગલંબાઈવાળો
(D) ઊંચી તીવ્રતાવાળો
જવાબ
(C) ટૂંકી તરંગલંબાઈવાળો

પ્રશ્ન 248.
500 nm તરંગલંબાઈ ધરાવતા પ્રકાશ વડે યંગની ડબલ લિટને પ્રકાશિત કરી છે.
તેમાના ઉપરના કિરણના માર્ગમાં 1.5 વક્રીભવનાંક ધરાવતી અને 2 µm જાડાઈ
ધરાવતી પાતળી ફિલ્મ દાખલ કરવામાં આવે તો મધ્યસ્થ પ્રકાશિત શલાકા (2003)
(A) જેમની તેમ જ રહેશે.
(B) બે શલાકા જેટલી નીચે ઊતરી જશે.
(C) બે શલાકા જેટલી ઉપર તરફ ખસી જશે.
(D) 10 શલાકા જેટલી નીચે તરફ ખસી જશે.
જવાબ
(C) બે શલાકા જેટલી ઉપર તરફ ખસી જશે. ફિલ્મને લીધે ઉદ્ભવતો પથ-તફાવત
Δx = µt – t
= (µ – 1) t
= (1.5 – 1) × 2 × 10-6
= 1 µm
હવે, Δx =
y =
શલાકાની પહોળાઈ W =
=
=
y =
= 2 ×
જે મધ્યસ્થ શલાકા બે શલાકાની પહોળાઈ સુધી ઉપર સ્થાનાંતરિત થશે.
પ્રશ્ન 249.
રેખીય ધ્રુવીભૂત પ્રકાશમાં રહેલા વિધુતક્ષેત્રના
(A) સમય સાથે બદલાતું નથી.
(B) સમય સાથે આવર્ત રીતે બદલાય છે.
(C) સમય સાથે સુરેખપણે વધે તથા ઘટે છે.
(D) પ્રસરણની દિશાને સમાંતર રહે છે.
જવાબ
(B) સમય સાથે આવર્ત રીતે બદલાય છે.
વિદ્યુતચુંબકીય તરંગમાં
પ્રશ્ન 250.
શાંત પાણીમાં પથ્થર નાખતાં તેની આસપાસ બહારની તરફ ત્રિજ્યાવર્તી વર્તુળાકાર
તરંગો ઉત્પન્ન થાય છે, તો આ ઘટનામાં કેન્દ્રથી ૪ અંતરે તેના તરંગોનો
કંપવિસ્તાર ……………………. ના સમપ્રમાણમાં બદલાય છે. (2006)
(A)
(B) r-1
(C) r-2
(D)
જવાબ
(B) r-1

પ્રશ્ન 251.
પાણીની સપાટી પર રહેલા તેલના પાતળા સ્તર પર સૂર્યપ્રકાશ (દિવસનો ઉજાસ કે
સફેદ પ્રકાશ) પડતાં તેમાં જુદા-જુદા રંગ જણાય છે. આ ઘટના ………………….. ની
છે.(2005)
(A) પ્રકાશના વ્યતિકરણ
(B) પ્રકાશના વિવર્તન
(C) પ્રકાશના વિભાજન
(D) પ્રકાશના ધ્રુવીભવન
જવાબ
(A) પ્રકાશનું વ્યતિકરણ
પાતળા સ્તરના વ્યતિકરણ અનુસાર સ્તરની જાડાઈ અને આપાત પ્રકાશના કોણને આધારે પ્રકાશના રંગ બદલાય છે.
પ્રશ્ન 252.
માધ્યમમાં પ્રસરતા તરંગો માટે કયો ગુણધર્મ એકબીજાથી સ્વતંત્ર છે ? (2006)
(A) વેગ
(C) આવૃત્તિ
(B) તરંગલંબાઈ
(D) તેઓ એકબીજા પર આધારિત છે.
જવાબ
(C) આવૃત્તિ
આવૃત્તિ એ ઉદ્ગમનો ગુણધર્મ છે, જે માધ્યમ પર આધારિત નથી.
પ્રશ્ન 253.
યંગના ડબલ લિટના પ્રયોગમાં, બંને સ્લિટ વચ્ચેનું અંતર વધારીને ત્રણ ગણું કરવામાં આવે તો શલાકાઓની પહોળાઈ ………………………. થાય. (2009)
(A) 9 ગણી
(B)
(C) 3 ગણી
(D)
જવાબ
(D)
યંગના ડબલ સ્વિટના પ્રયોગમાં, શલાકાની પહોળાઈ
β =
d’ = 3d લેતાં,
β’ =
β’ =
પ્રશ્ન 254.
વિવર્તન ગ્રેટિંગ પર પ્રકાશના કિરણજૂથને લંબરૂપે આપાત કરતા, પ્રથમ વિવર્તન કોણ 32° હોય તો, દ્વિતીય વિવર્તન કોણ ………………….. (2009)
(A) 80°
(B) 64°
(C) 48°
(D) શક્ય નથી.
જવાબ
(D) શક્ય નથી.
એક જ સ્લિટ વડે થતાં ફ્રોનહોફર વિવર્તનમાં,
d sin θn = nλ
પ્રથમ ક્રમ માટે
∴ d sin 32° = 1 × λ ⇒ λ = d sin 32°
હવે, બીજા ક્રમ માટે,
d sin θ2 = 2 × λ
∴ d sin θ2 = 2 × d sin 32°
∴ sin θ2 = 2 × sin 32°
= 2 × 0.529
sin θ2 = 1.06
પરંતુ, ખૂણાનું sin મૂલ્ય 1 કરતાં કદી વધુ હોઈ શકે નહીં માટે, બીજા ક્રમનું વિવર્તન થાય નહીં.
પ્રશ્ન 255.
નીચે આપેલા વિકલ્પોમાંથી કયો વિકલ્પ સુસમ્બદ્ધ ઉદ્ગમ નથી ? (2009)
(A) લૉઇડ મી૨૨
(B) ફ્રેનલ પ્રિઝમ
(C) યંગની ડબલ સ્લિટ
(D) પ્રિઝમ
જવાબ
(D) પ્રિઝમ
પ્રશ્ન 256.
યંગના ડબલ સ્લિટ વડે થતા વ્યતિકરણના પ્રયોગમાં બંને સ્લિટ સુસમ્બદ્ધ ઉદ્ગમ
તરીકે વર્તે છે. જેમાંથી આવતા પ્રકાશનો કંપવિસ્તાર ‘a’ અને તરંગલંબાઈ λ છે.
બીજા યંગના ડબલ સ્વિટના પ્રયોગમાં બંને ઉદ્ગમો સુસમ્બા નથી, પરંતુ
કંપવિસ્તાર ‘a’ અને તરંગલંબાઈ λ જ છે, તો પડદાના મધ્યબિંદુએ પ્રથમ અને
દ્વિતીય કિસ્સામાં મળતી તીવ્રતાઓનો ગુણોત્તર = …………………… (2009)
(A) 2 : 1
(B) 1 : 2
(C) 3 : 4
(D) 4 : 3
જવાબ
(A) 2 : 1
સુસમ્બદ્ધ ઉદ્ગમો માટે પડદાના મધ્યબિંદુએ પ્રકાશીય તીવ્રતા
Imax = (a + a)2 = 4a2
હવે, અસુસંબદ્ધ ઉદ્ગમો વ્યતિકરણ ઉપજાવતાં ન હોવાથી, પડદાના મધ્યબિંદુએ પ્રકાશીય તીવ્રતા
I = I1 + I2 ⇒ a2 + a2 = 2a2
∴
પ્રશ્ન 257.
500 nm તરંગલંબાઈવાળા પ્રકાશ તથા 0.1 mm ના વ્યાસવાળા લેન્સ વડે એક જ સ્લિટ
વડે થતા વિવર્તનના કિસ્સામાં 1m દૂર રાખેલા પડદા પર મળતા મધ્યસ્થ
અધિક્તમની પહોળાઈ ………………….. હોય. (2011)
(A) 5 mm
(B) 1mm
(C) 10 mm
(D) 2.5 mm
જવાબ
(C) 10 mm
મધ્યસ્થ અધિકતમની પહોળાઈ એટલે તેની બંને બાજુના પ્રથમ ન્યૂનતમ વચ્ચેનું અંતર. ∴ મધ્યસ્થ અધિકતમની પહોળાઈ
2sin V1 =
=
= 10 × 10-1 cm = 10 mm
સૂચના :
(a) વિધાન અને કારણ બંને સાચાં છે અને વિધાન માટે કારણ સાચી સમજૂતી છે.
(b) વિધાન અને કારણ બંને સાચાં છે પરંતુ કારણ એ વિધાનની સમજૂતી નથી.
(c) વિધાન સાચું પરંતુ કારણ ખોટું છે.
(d) વિધાન અને કારણ બંને ખોટાં છે.
પ્રશ્ન 258.
વિધાન : હવા અને પાણીમાં પ્રકાશના વેગને સમજાવવામાં કણવાદ નિષ્ફળ છે.
કારણ : કણવાદ અનુસાર ઘટ્ટ માધ્યમમાં પ્રકાશ, પાતળા માધ્યમ કરતાં ઝડપથી ગતિ કરે છે. (2012)
(A) a
(B) b
(C) c
(D) d
જવાબ
(A) a
પ્રશ્ન 259.
વિધાન : બે વાયોલીનમાંથી ઉત્પન્ન થતાં ધ્વનિના તરંગો વચ્ચે વ્યતિકરણ રચાવું શક્ય નથી.
કારણ : વ્યતિકરણ માટે બે તરંગોની કળાનો તફાવત અચળ રહેવો જોઈએ. (2012)
(A) a
(B) b
(C) c
(D) d
જવાબ
(A) a
પ્રશ્ન 260.
વિધાન : પ્રકાશનું વિવર્તન જોવા માટે અડચણ 107m ના ક્રમની હોવી જોઈએ.
કારણ : દૃશ્ય પ્રકાશની તરંગલંબાઈ 10-7 mના ક્રમની હોય છે. (2012)
(A) a
(B) b
(C) c
(D) d
જવાબ
(A) a
પ્રશ્ન 261.
વિધાન : ટેલિસ્કોપની વિભેદનશક્તિ વધારવા માટે ઓબ્જેક્ટિવનો વ્યાસ મોટો હોવો જોઈએ.
કારણ : ટેલિસ્કોપની વિભેદનશક્તિ
(A) a
(B) b
(C) c
(D) d
જવાબ
(A) a
પ્રશ્ન 262.
પ્રકાશના ધ્રુવીભવન દરમિયાન શું બદલાય છે ? (GUJCET Mock Test – 2006)
(A) આવૃત્તિ
(B) તરંગલંબાઈ
(C) કળા
(D) તીવ્રતા
જવાબ
(D) તીવ્રતા
પ્રકાશની તીવ્રતા તેના તરંગ સ્વરૂપમાં, લંબગત તરંગના કંપવિસ્તાર પર આધાર
રાખે છે. અવીભૂત પ્રકાશમાં બંને ઘટકો હોવાથી તેની તીવ્રતા વધુ હોય છે.
અવીભૂત પ્રકાશનું ધ્રુવીભવન થતાં ધ્રુવીભૂત પ્રકાશ, પ્રસરણને લંબ સમતલના
ચોક્કસ દિશામાંના ઘટકો જ ધરાવતો હોવાથી તેની તીવ્રતા હંમેશાં ઓછી હોય છે.
પ્રશ્ન 263.
એક પોલેરોઇડની દક્-અક્ષ સાથે 45° ના ખૂણે I0 તીવ્રતાવાળો પ્રકાશ આપાત કરવામાં આવે છે, તો નિર્ગમન પામતા પ્રકાશની તીવ્રતા ………………… (Mock Test – 2006)
(A) I0
(B) 0.5 I0
(C) 0.25 I0
(D) શૂન્ય
જવાબ
(B) 0.5 I0
માલસના નિયમ પરથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા
I = I0cos2θ
= I0cos245°
= I0 ×
પ્રશ્ન 264.
વ્યતિકરણના પ્રયોગમાં 700 nm તરંગલંબાઈવાળા પ્રકાશથી જે બિંદુએ ત્રીજા
ક્રમની પ્રકાશિત શલાકા મળે તે જ બિંદુએ 5મી પ્રકાશિત શલાકા મેળવવા પ્રકાશની
તરંગલંબાઈ કેટલી હોવી જોઈએ ? (2006)
(A) 420 nm
(B) 500 nm
(C) 750 nm
(D) 630 nm
જવાબ
(A) 420 nm
n1λ1 = n2λ2
∴ λ2 = λ1 ×
= 700 ×
પ્રશ્ન 265.
પ્રકાશના ધ્રુવીભવન વડે સાબિત થાય છે કે પ્રકાશ …………………… નો બનેલો છે. (2007)
(A) લંબગત તરંગો
(B) સંગત તરંગો
(C) સુરેખ તરંગો
(D) તરંગ વગરનાં કિરણો
જવાબ
(A) લંબગત તરંગો
પ્રશ્ન 266.
પ્રકાશીય ઉપકરણની વિભેદન મર્યાદા …………………. ના લીધે ઉદ્ભવે છે. (2007)
(A) વ્યતિકરણ
(C) વિવર્તન
(B) ધ્રુવીભવન
(D) પરાવર્તન
જવાબ
(C) વિવર્તન
પ્રશ્ન 267.
પાણીમાં ગતિ કરતું પ્રકાશનું કિરણ પાણીમાં ડુબાડેલ ગ્લાસ પ્લેટ પર આપાત થાય
છે. જ્યારે આપાતકોણ 51° નો બને છે, ત્યારે પરાવર્તિત કિરણ સંપૂર્ણ
તલધ્રુવીભૂત બને છે, તો કાચનો વક્રીભવનાંક કેટલો થશે ? (પાણીનો વક્રીભવનાંક
1.3 અને tan 51° = 1.235) (2008)
(A) 1.33
(B) 1.805
(C) 1.605
(D) 1.305
જવાબ
(C) 1.605
∴ ng = nωtan51°
= 1.3 × 1.235 = 1.6055 ≈ 1.605
પ્રશ્ન 268.
એક ટેલિસ્કોપના લેન્સનો વ્યાસ 0.61 m છે, પ્રકાશની તરંગલંબાઈ 5000 Å છે, તો ટેલિસ્કોપની વિભેદનશક્તિ …………………………. છે. (2008)
(A) 2 × 104
(B) 2× 102
(C) 2 × 106
(D) 106
જવાબ
(D) 106
ટેલિસ્કોપની વિભેદનશક્તિ =
=
પ્રશ્ન 269.
યંગના બે લિટના પ્રયોગમાં બે લિટ વચ્ચેનું અંતર 0.28 mm અને લિટ તથા પડદા
વચ્ચેનું અંતર 1.4 m છે. જો મધ્યસ્થ પ્રકાશિત શલાકા અને ત્રીજી પ્રકાશિત
શલાકા વચ્ચેનું અંતર 0.9 cm હોય, તો આ પ્રયોગમાં વપરાયેલ પ્રકાશની
તરંગલંબાઈ કેટલી ? (2009)
(A) 6000Å
(B) 5000Å
(C) 4000Å
(D) 3000Å
જવાબ
(A) 6000Å
sin θ3 =
∴ λ =
= 6 × 10-5 cm = 6000Å
પ્રશ્ન 270.
નીચેનામાંથી કોનું ધ્રુવીભવન થઈ શકતું નથી ? (2009)
(A) અલ્ટ્રાસોનિક તરંગો
(B) રેડિયો તરંગો
(C) પારજાંબલી કિરણો
(D) ક્ષ-કિરણો
જવાબ
(A) અલ્ટ્રાસોનિક તરંગો
આ સિવાયના તરંગો વિદ્યુતચુંબકીય તરંગો છે, જે લંબગત છે.
પ્રશ્ન 271.
100 કળાતફાવત = ………………….. પથતફાવત. (2010)
(A) 50 λ
(B) 100 λ
(C) 10 λ
(D) 25 λ
જવાબ
(A) 50 λ
કળાતફાવત = k × પથતફાવત
∴ કળાતફાવત =
=
= 50 λ
પ્રશ્ન 272.
500 nm તરંગલંબાઈવાળા પ્રકાશ દ્વારા 0.50 mm પહોળાઈની સ્લિટ દ્વારા મળતા
ફ્રોનહોફર વિવર્તનમાં પ્રથમ ક્રમના મહત્તમનો વિવર્તન કેટલો ? (2010)
(A) 1.5 × 10-4 રેડિયન
(B) 1.5 × 10-3 રેડિયન
(C) 1 × 10-3 રેડિયન
(D) 3 × 10-3 રેડિયન
જવાબ
(D) 3 × 10-3 રેડિયન
‘m’ મા ક્રમના અધિકતમ માટેની શરત
d sin θm = (2m + 1)
m = 1 લેતાં,
sin θ1 =
=
જો θ1 ઘણો નાનો હોય, તો sin θ1 ≈ θ1
θ1 = 3 × 10-3 રેડિયન
પ્રશ્ન 273.
વ્યતિકરણના યંગના બે સ્વિટના પ્રયોગની ગોઠવણીને હવામાંથી પાણીમાં લઈ જતાં તેની શલાકાની પહોળાઈ ………………….. (2011)
(A) અનંત બને છે.
(B) ઘટે છે.
(C) વધે છે.
(D) બદલાતી નથી.
જવાબ
(B) ઘટે છે.
શલાકાની પહોળાઈ (2
કરતાં પ્રકાશની તરંગલંબાઈ ઘટે છે તેથી શલાકાની પહોળાઈ પણ ઘટે છે.
પ્રશ્ન 274.
તલધ્રુવીભૂત પ્રકાશના કિરણ જૂથના પ્રસરણમાં ધ્રુવીભવનતલ અને પ્રસરણની દિશા વચ્ચેનો ખૂણો કેટલો છે ? (2012)
(A) 0°
(B) 45°
(C) 180°
(D) 90°
જવાબ
(A) 0°
પ્રશ્ન 275.
રંગના બે લિટના પ્રયોગમાં, પડદા પરના કોઈ બિંદુ P પરની તીવ્રતા
વ્યતિકરણભાતમાં મળતી મહત્તમ તીવ્રતા કરતાં અડધી છે. જો વાપરેલ તરંગલંબાઈ λ
હોય અને બે સ્લિટ વચ્ચેનું અંતર d હોય તો પડદા પરના બિંદુ P અને મધ્યસ્થ
શલાકા વચ્ચેનું કોણીય અંતર કેટલું હશે ? (2012)
(A) sin-1(
(B) sin-1(
(C) sin-1(
(D) sin-1(
જવાબ
(C) sin-1(

પ્રશ્ન 276.
બે મેલિન પ્લેટના પ્રયોગમાં પોલેરાઇઝર અને એનેલાઇઝર ક્રૉસ્ડ છે. હવે
એનેલાઇઝરને કેટલી ફેરવવી પડે કે જેથી પોલેરાઇઝરમાંથી બહાર આવતા પ્રકાશના
25% એનેલાઇઝરમાંથી પસાર થાય ? (2012)
(A) 60°
(B) 90°
(C) 30°
(D) 45°
જવાબ
(C) 30°
માલસના નિયમ પરથી
I = I0cos2θ [I – I0 ના 20% =
∴ θ = 60°
∴ એનેલાઇઝરને = (90° – 60°) = 30° જેટલી ફેરવવી પડે.
પ્રશ્ન 277.
ગંગના પ્રયોગની ગોઠવણીમાં 1.5 વક્રીભવનાંકવાળી કાચની પ્લેટ દાખલ કરવામાં
આવે ત્યારે 6000Å તરંગલંબાઈના પ્રકાશથી મળતી વ્યતિકરણ ભાતની મધ્યસ્થ શલાકા,
4 થા ક્રમની અપ્રકાશિત શલાકા પર સંપાત થાય છે, તો કાચની પ્લેટની જાડાઈ
કેટલી હશે ? (2013)
(A) 6 × 10-6m
(B) 4.5 × 10-6m
(C) 4.2 × 10-6m
(D) 4.8 × 10-6m
જવાબ
(C) 4.2 × 10-6m

પ્રશ્ન 278.
I1 અને I2 તીવ્રતાવાળા પ્રકાશના બે કિરણજૂથ વ્યતિકરણ ભાત રચે છે. જો તેમની મહત્તમ અને ન્યૂનતમ તીવ્રતાઓનો
ગુણોત્તર
(B) 4 : 1
(C) 1 : 4
(D) 9 : 1
(A) 1 : 9
જવાબ
(D) 9 : 1


પ્રશ્ન 279.
વ્યતિકરણ માટેના યંગના પ્રયોગમાં જો ચોથી પ્રકાશિત શલાકાની પહોળાઈ 2 × 10-2 cm હોય, તો છઠ્ઠી પ્રકાશિત શલાકાની પહોળાઈ ……………….. cm થાય. (2014)
(A) 3 × 10-2
(B) 10-2
(C) 2 × 10-2
(D) 1.5 × 10-2
જવાબ
(C) 2 × 10-2
વ્યતિકરણ શલાકાઓ સમાન તીવ્રતાની અને સમાન પહોળાઈની હોય છે.
પ્રશ્ન 280.
માનવઆંખની કીકીનો વ્યાસ 2.5 mm છે. પ્રકાશની તરંગલંબાઈ 5000Å છે. માનવઆંખ
ઓછામાં ઓછા એકબીજાથી કેટલા અંતરે રહેલી બિંદુવત્ વસ્તુઓને છૂટી છૂટી જોઈ
શકે ? આંખ અને વસ્તુઓ વચ્ચેનું અંતર 5 m છે. (2014)
(A) 1.22 × 10-3m
(B) 1.34 × 10-3m
(C) 1.5 × 10-3m
(D) 1.6 × 10-3m
જવાબ
(A) 1.22 × 10-3m
x =
=
પ્રશ્ન 281.
અધ્રુવીભૂત પ્રકાશ, પોલેરાઇઝર P પર આપાત થાય છે. પોલેરાઇઝરમાંથી નિર્ગમન
પામતો પ્રકાશ એનેલાઇઝર A પર આપાત થાય છે. જો એનેલાઇઝરમાંથી નિર્ગમન પામતા
પ્રકાશની તીવ્રતા, આપાત અધ્રુવીભૂત પ્રકાશની તીવ્રતા કરતાં
(A) 45°
(B) 30°
(C) 0°
(D) 60°
જવાબ
(D) 60°
I =
∴ θ = 60°
પ્રશ્ન 282.
એક ટૂર્મેલિન પ્લેટ પર તલ-ધ્રુવીભૂત પ્રકાશ આપાત થાય છે. ટૂર્મેલિન પ્લેટની પ્રકાશીય અક્ષ સાથે તેના
(A) 25%
(B) 75%
(C) 50%
(D) 90%
જવાબ
(B) 75%
I = I0cos2θ
I0cos260°
I =
=
પ્રશ્ન 283.
λ તરંગલંબાઈનો પ્રકાશ d પહોળાઈની સ્લિટ પર આપાત થાય છે. D અંતરે રહેલ પડદા
પર પરિણામી વિવર્તન ભાત રચાય છે. મધ્યસ્થ અધિકતમની પહોળાઈ એ સ્વિટની પહોળાઈ
જેટલી હોય તો D = ………………… (2015)
(A)
(B)
(C)
(D)
જવાબ
(A)
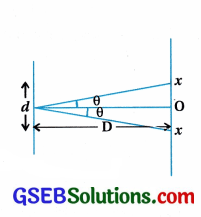
પ્રથમ ક્રમના વિવર્તન માટે,
dsinθ = λ
નાના ખૂણા માટે,
d(θ) = λ
∴ Q ની બંને બાજુના પ્રથમ ક્રમના
વિવર્તન માટે,
d(2θ) = 2λ
પણ θ =
∴ d(
∴
∴
∴ D =
પ્રશ્ન 284.
જો પ્રકાશની તરંગલંબાઈ 4000 Å હોય, તો 1mm લંબાઈમાં રહેલા તરંગોની સંખ્યા …………………. હશે. (2015)
(A) 25
(B) 250
(C) 2500
(D) 25000
જ્વાબ
(C) 2500
તરંગોની સંખ્યા n =
=
= 0.25 × 104 = 2500
પ્રશ્ન 285.
2 વક્રીભવનાંક ધરાવતા માધ્યમમાં 5000 Å તરંગલંબાઈવાળા વિદ્યુતચુંબકીય તરંગનો વેગ …………………… m/s છે. (2016)
(A) 2 × 108
(B) 1.5 × 108
(C) 3 × 108
(D) 1.5 × 109
જવાબ
(B) 1.5 × 108
n =
∴ v =
પ્રશ્ન 286.
વાદળી પ્રકાશની મદદથી વિવર્તન મેળવવામાં આવે છે. હવે જો વાદળી પ્રકાશના બદલે પીળો પ્રકાશ વાપરવામાં આવે તો …………………… (2016)
(A) અધિકતમો અને ન્યૂનતમો પહોળા અને એકબીજાથી દૂર જાય છે.
(B) અધિકતમો અને ન્યૂનતમો સાંકડા અને વધારે ગીચ થાય છે.
(C) વિવર્તન ભાતમાં કોઈ ફેરફાર થતો નથી.
(D) વિવર્તન ભાત અદશ્ય થાય છે.
જવાબ
(A) અધિકતમો અને ન્યૂનતમો પહોળા અને એકબીજાથી દૂર જાય છે.
વિવર્તનનો આધાર
∴ વિવર્તન ∝ λ અને λv < λy
તેથી પીળા રંગના પ્રકાશથી વિવર્તન વધુ થશે જેથી મધ્યસ્થ અધિકતમો અને ન્યૂનતમો પહોળા થશે અને એકબીજાથી દૂર જશે.
પ્રશ્ન 287.
એક લિટથી થતા ફ્રોનહોફર વિવર્તનમાં લિટની પહોળાઈ 001 cm છે. જો સ્વિટને
લંબરૂપે આપાત પ્રકાશની તરંગલંબાઈ 5000 Å હોય, તો દ્વિતીય અધિકતમનું મધ્યસ્થ
અધિક્તમની મધ્યરેખાથી કોણીય અંતર ……………………. rad હશે. (2016)
(A) 0.125
(B) 0.15
(C) 0.015
(D) 0.0125
જવાબ
(D) 0.0125
‘n’ મા ક્રમના અધિકતમ માટે,
d sinθ = (2n + 1)
∴ sinθ = (2n + 1)
=
=
પ્રશ્ન 288.
યંગના વ્યતિકરણના પ્રયોગમાં જો બે લિટો વચ્ચેનું અંતર વપરાયેલ પ્રકાશની
તરંગલંબાઈ જેટલું જ હોય તો પડદા પર વધારેમાં વધારે કેટલી પ્રકાશિત શલાકાઓ
મળે ? (2017)
(A) 3
(B) 5
(C) 7
(D) અનંત
જવાબ
(A) 3
પ્રકાશિત (અધિકતમ)ની શરત
dsinθ = nλ
∴ λsinθ = nλ [∵ d = λ]
∴ sinθ = n
પણ sinθ ≤ 1 હોવાથી n ≤ 1
∴ n ના શક્ય મૂલ્ય −1, 0, 1
∴ કુલ ત્રણ અધિકતમ શલાકાઓ મળે.
પ્રશ્ન 289.
10 cm વ્યાસના ઓબ્જેક્ટિવવાળા ટેલિસ્કોપનું કોણીય વિભેદન ………………….. rad છે. (પ્રકાશની તરંગલંબાઈ 6000 Å લો) (2017)
(A) 6.10 × 10-6
(B) 7.32 × 10-6
(C) 6.55 × 10-6
(D) 7.52 × 10-6
જવાબ
(B) 7.32 × 10-6
ટેલિસ્કોપની કોણીય વિભેદનશક્તિ
αmin =
=
= 7.32 × 10-6
પ્રશ્ન 290.
યોગ્ય રીતે કોલમ I સાથે કોલમ II જોડો.

(2018)
(A) i → P, ii → S, iii → R, iv → Q
(B) i → P, ii → R, iii → S, iv → Q
(C) i → Q, ii → S, iii → R, iv → P
(D) i → R, ii → Q, iii → S, iv → P
જવાબ
(B) i → P, ii → R, iii → S, iv → Q
પ્રશ્ન 291.
વ્યતિકરણ શલાકાઓ માટે નીચેનામાં શું ખોટું છે ? (2018)
(A) શલાકાઓ તરંગઅગ્રના મર્યાદિત ભાગને લીધે મળે છે.
(B) બીધી જ પ્રકાશિત શલાકાઓ સમાન પ્રકાશિત હોય છે.
(C) બે ક્રમિક શલાકાઓ વચ્ચેનું અંતર અચળ હોય છે.
(D) શલાકાઓ સુસંબદ્ધ ઉદ્ગમોને લીધે મળે છે.
જવાબ
(A) શલાકાઓ તરંગ અગ્રના મર્યાદિત ભાગને લીધે મળે છે.
તરંગ અગ્રના મર્યાદિત ભાગના લીધે વ્યક્તિકરણ નહિ પણ વિવર્તન શલાકાઓ મળે.
પ્રશ્ન 292.
અશુદ્ધ પાણીમાં ગતિ કરતું પ્રકાશનું કિરણ અશુદ્ધ પાણીમાં ડુબાડેલી ગ્લાસ
પ્લેટ પર આપાત થાય છે જ્યારે આપાતકોણ 51° નો બને છે ત્યારે પરાવર્તિત કિરણ
સંપૂર્ણ તલધ્રુવીભૂત બને છે તો ગ્લાસ (કાચ) નો વક્રીભવનાંક કેટલો ? અશુદ્ધ
પાણીનો વક્રીભવનાંક = 1.4 લો (tan 51° = 1.235) (2018)
(A) 1.64
(B) 1.34
(C) 1.53
(D) 1.73
જવાબ
(D) 1.73
n = tan θp = tan 51° = 1.235
n =
= 1.235 × 1.4 = 1.729 ≈ 1.73
પ્રશ્ન 293.
બે લિટો વચ્ચેનું અંતર 3 mm અને પડદો 2 m દૂર રાખવામાં આવે છે. જ્યારે 500
nm તરંગલંબાઈનો બ્લૂ ગ્રીન પ્રકાશ વાપરવામાં આવે તો શલાકાઓ વચ્ચેનું અંતર
કેટલું થશે ? (2020)
(A) 0.33 mm
(B) 0.43 mm
(C) 0.5 mm
(D) 0.4 mm
જવાબ
(A) 0.33 mm
પાઠ્યપુસ્તક પ્રકરણ નં. 10 ના ઉદાહરણનો દાખલા નં. 10.3જેવો.
બે ક્રમિક શલાકા વચ્ચેનું અંતર,
β =
પ્રશ્ન 294.
જ્યારે અડચણની પહોળાઈ 4 mm હોય અને તરંગલંબાઈ 500 nm હોય તો કયા અંતર માટે કિરણ પ્રકાશશાસ્ત્ર એક સારી સંનિકટતા હશે ? (2020)
(A) 18m
(B) 32 m
(C) 8m
(D) 6 m
જવાબ
(B) 32 m
ફેનલ લંબાઈ Zf =
પ્રશ્ન 295.
માઇક્રોસ્કોપની વિભેદનશક્તિ ………………….. હોય છે. (2020)
(A)
(B)
(C)
(D)
જવાબ
(D)
માઇક્રોસ્કોપનું વિભેદન dm =
જો વસ્તુ અને વસ્તુકાચની વચ્ચે “n” વક્રીભવનાંકવાળું માધ્યમ રાખેલ હોય તો dm =
માઇક્રોસ્કોપની વિભેદનશક્તિ (R.P)
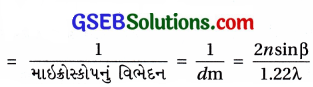
આથી પ્રશ્નમાં ભૂલ હોઈ શકે અને માઇક્રોસ્કોપની વિભેદનશક્તિના બદલે
માઇક્રોસ્કોપનું વિભેદન હોવું જોઈએ. આથી બૉર્ડે Answer key માં ફૂદડી (*)
મૂકી છે.
પ્રશ્ન 296.
યંગના બે સ્લિટના પ્રયોગમાં, ઉદ્ગમ સ્લિટની પહોળાઈ વધારવામાં આવે તો …………………. (માર્ચ 2020)
(A) વ્યતિકરણભાત વધુ ને વધુ સ્પષ્ટ થતી જાય છે.
(B) શલાકાઓ વચ્ચેના કોણીય અંતર વધે છે.
(C) વ્યતિકરણને સ્થાને વિવર્તન જણાય છે.
(D) વ્યતિકરણભાત ઓછી અને ઓછી સ્પષ્ટ થતી જાય છે.
જવાબ
(D) વ્યતિકરણભાત ઓછી અને ઓછી સ્પષ્ટ થતી જાય છે.
પ્રશ્ન 297.
જ્યારે ઉદ્ગમ અવલોકનકારથી દૂર ખસતો હોય ત્યારે vત્રિજ્યાવર્તી ને ………………… ગણવામાં આવે છે. (માર્ચ 2020)
(A) ધન
(C) ઋણ
(B) શૂન્ય
(D) અનંત
જવાબ
(A) ધન
પ્રશ્ન 298.
ધારો કે તારામાંથી 6000 Å તરંગલંબાઈનો પ્રકાશ આવે છે. જેના ઑબ્જેક્ટિવનો
વ્યાસ 254 cm હોય તેવા ટેલિસ્કોપ માટે વિભેદન સીમા શું હશે ? (ઑગષ્ટ 2020)
(A) 2.9 × 10-6 રેડિયન
(B) 2.9 × 107 રેડિયન
(C) 2.9 × 106 રેડિયન
(D) 2.9 × 10-7 રેડિયન
જવાબ
(D) 2.9 × 10-7 રેડિયન
પ્રશ્ન 299.
જ્યારે અડચણની પહોળાઈ ૩mm હોય અને તરંગલંબાઈ 500 nm હોય તો કયા અંતર માટે કિરણ પ્રકાશશાસ્ત્ર એક સારી સંનિકટતા હશે ? (ઑગષ્ટ 2020)
(A) 18 cm
(B) 18 m
(C) 1.8m
(D) 1.8 cm
જવાબ
(B) 18 m
પ્રશ્ન 300.
અધુવીભૂત પ્રકાશ એક સમતલ કાચની સપાટી પર આપાત થાય છે. પરાવર્તિત અને
વક્રીભૂત કિરણો એકબીજાને લંબ થાય તે માટે આપાતકોણ કેટલો હશે ? (µ = 1.54
લો) (ઑગષ્ટ 2020)
(A) 57°
(B) 55°
(C) 30°
(D) 45°
જવાબ
(A) 57°
પ્રશ્ન 301.
પાણીનો વકીભવનાંક
(A) 4 × 108 ms-1
(B) 3 × 108 ms-1
(C) 2.25 × 108 ms-1
(D) 2 × 108 ms-1
જવાબ
(C) 2.25 × 108ms-1
η =
c = શૂન્યાવકાશમાં પ્રકાશની ઝડપ
∴ v =
પ્રશ્ન 302.
પ્રકાશનું કિરણ લંબગત છે તેવું …………………….. પ્રકાશીય ઘટનાથી જાણી શકાય છે. (ઑગષ્ટ 2020)
(A) વ્યતિકરણ
(B) પરાવર્તન
(C) વિવર્તન
(D) ધ્રુવીભવન
જવાબ
(D) ધ્રુવીભવન

0 Comments