CHAPTER 8 - ELECTROMAGNETIC WAVES
Displacement Current
Displacement current is the current that is produced by the rate of change of the electric displacement field. It differs from the normal current that is produced by the motion of the electric charge. Displacement current is the quantity explained in Maxwell’s Equation. It is measured in Ampere. Displacement currents are produced by a time-varying electric field rather than moving charges.
In this article we will learn about, displacement current, its characteristics, and others in detail.
What is Displacement Current?
Electricity and magnetism are related to each other. As the electric current travels through a wire, it creates magnetic field lines around the wire. This type of current is called conduction current, which is created by the movement of electrons through a conductor such as an electrical wire.
Whereas a displacement current is a type of current linked with Maxwell’s Equation and is produced by a time-varying electric field.
Displacement Current Definition
A physical quantity related to Maxwell’s equation that has the property of the electric current is called the Displacement Current. Displacement current is defined as the rate of change of the electric displacement field (D).
Maxwell’s equation includes displacement current that proves the Ampere Circuit Law. It is measured in Ampere.
Current in Capacitor
A charging capacitor has no conduction of charge but the charge accumulation in the capacitor changes the electric field link with the capacitor that in turn produces the current called the Displacement Current.
ID = JDS = S(∂D/∂t)
where,
- S is the area of the Capacitor Plate
- ID is the Displacement Current
- JD is the Displacement Current Density.
- D is related to Electric Field E as,
D = εE
- ε is the Permittivity of material between plates
Displacement Current Equation
Maxwell’s Equation defines the displacement current which has the same unit as the electric current, the Maxwell field equation is represented as,
∇×H = J + JD
where,
H is related to magnetic field B as B = μH
μ is the permeability of the material between the plates
J is the Conducting Current Density.
JD is the Displacement Current Density.
We know that
∇.(∇×H) = 0
∇.J = -∂ρ/∂t
∇.J = -∇.∂D/∂t
Using Gauss’s Law
∇.D = ρ
Here, ρ is the electric charge density.
Thus the displacement current density equation is,
JD = ∂D/∂t
Characteristics of Displacement Current
In an electric circuit, there are two types of current that are conduction current and the other is Displacement current. Various characteristics of displacement current are mentioned below:
- Displacement current does not appear from the actual movement of the electric charge as in the case of the conduction current but is produced by time changing electric field.
- Displacement current is a vector quantity.
- Electromagnetic waves propagate with the help of displacement current
Electromagnetic Waves (EM)
Electromagnetic Waves are a combination of electric and magnetic field waves produced by moving charges. EM waves are created by the oscillation of electrically charged particles (accelerating charges). The electric field associated with the accelerating charge vibrates due to which a vibrating magnetic field is generated. These vibrating electric and magnetic fields give rise to EM waves. Both the electric and magnetic fields in an electromagnetic wave will fluctuate in time, one causing the other to change.
Nature of Electromagnetic Waves
In an electromagnetic wave, the electric field and magnetic field are perpendicular to each other and at the same time are perpendicular to the direction of propagation of the wave, this nature of EM wave is known as Transverse nature. In these transverse waves, the direction of disturbance or displacement in the medium is perpendicular to that of the propagation of the wave. The particles of the medium oscillate in a direction perpendicular to the direction of propagation of the wave. Because of this EM waves are transverse in nature.
The electric field of the EM wave is represented as
EY = E0sin (kx – ωt)
where,
EY = electric field along the y-axis,
x = direction of propagation of the wave
Wave number k = (2π / λ).
The magnetic field of the EM wave is represented as
BZ = B0sin(kx – ωt)
where,
BZ = magnetic field along the z-axis
x = direction of propagation of the wave
Wave number k = (2π / λ)
Faraday’s Law
This law is stated as when an electromotive force is induced in a coil or a circuit when there is a magnetic field varying with time, or there is a rate of change in magnetic flux through the coil. Using Lenz’s law we can determine the direction of the induced emf. It suggests that the induced emf always opposes the cause of its formation in the first place.
The relation between the emf ε in a wire and the electric field E in the wire is given by,
ε = ∫ E . dl
Where, dl is the element of the contour of the surface, combining this with the definition of flux,
φB = ∫ B . dA
The integral form of the above equation can be written as,
∫ E . dl = -d/dt ∫ B . dA
Maxwell-Ampere Law
The progress in the theory of displacement current can be traced back to a famous physicist named James Clerk Maxwell. Maxwell is well known for Maxwell’s Equations. The combination of four equations demonstrates the fundamentals of electricity and magnetism. For displacement current, we will be focusing on one of these equations known as the Maxwell-Ampere law.
Before Maxwell, Andre-Marie Ampere had developed the famous equation known as Ampere’s law. This law relates the magnetic field (B) surrounding a closed loop to the conduction current (I) traveling through that loop multiplied by a constant known as the permeability of free space (μ0).
∫B . ds = μ0I
Whenever there is continuous conduction current Ampere’s law holds true, but there are cases when problems arise in the law as it’s written. For example, a circuit with a capacitor in it. When the capacitor is charging and discharging, current flows through the wires creating a magnetic field, but between the plates of the capacitor, there is no presence of current flow. According to Ampere’s law, there can be no magnetic field created by the current here, but we know that a magnetic field does exist. Maxwell realized this discrepancy in Ampere’s law and modified it in order to resolve the issue.
∫B . ds = μ0 (I + ε0 (dφE /dt))
This final form of the equation is known as the Maxwell-Ampere law.
The part Maxwell added to it is known as displacement current (Id), and the formula is,
Id = ε0 (dφE /dt)
The above equation consists of two terms multiplied together. The first is known as the permittivity of free space (ε0), and the second is the derivative with respect to time and electric flux (φE). Electric flux is the rate of flow of an electric field through a given area. By taking its derivative with respect to time, we consider the change in that rate of flow over time.
Displacement Current using Maxwell’s Equation
Maxwell adjusted the main relation of Ampere’s Circuital Law with an additional term. This made the relationship complete and wholesome with both static and time-varying parts present to play their part. Determination of displacement can be done using,
At first, take the magnetic field intensity without the magnetism,
B = μH
Addition of an additional term (Jd) in the above equation,
∇ × H = J + Jd
Performing the divergence action,
∇ . (∇ × H) = 0 = ∇ . J + ∇ . Jd
To define the Jd term,
∇ . Jd = -∇ . J
∇ . Jd = ∂pv / ∂t………….(1)
Using Gauss’s law, ∇ . D = p, Where D is the displacement vector and p is the charge density. Equation (1) becomes,
∂pv / ∂t = (∂ / ∂t) (∇ . D) = ∇ . (∂D / ∂t)
∇ . Jd = ∇ . (∂D / ∂t)
Therefore,
Jd = ∇ . (∂D / ∂t)
This derived term is known as the displacement current density formula. This comes in use when time-varying fields are required. For a constant displacement vector, i.e. a constant charge density the displacement current density vanishes.
So, the integral form of Maxwell’s equation is,
∫E . da = Q / ε0
∫B . da = 0
∫E . dl = -∫δB / δt. (da)
∫B . dl = μ0 l + μ0ε0 ∫(∂E / ∂t)
Need for Displacement Current
Ampere’s circuital law for conduction of current during charging of a capacitor was found inconsistent. Therefore, Maxwell modified Ampere’s circuital law by introducing the concept of displacement current.
Displacement currents play a central role in the propagation of electromagnetic radiation, such as light and radio waves through empty space. It is required to make the conduction current lead in the circuit. Conduction current in wires can be made to lead the voltage by means of displacement current inside the capacitor and it has vast uses in induction motors, industrial appliances, and in our day-to-day life.
Read More,
Solved Examples on Displacement Current
Example 1: Instantaneous displacement current of 2.0 A is set up in the space between two parallel plates of a 1 μF capacitor. find the rate of change in potential difference across the capacitor.
Solution:
In a Capacitor
V = q/C
dV/dt = i/C
dV/dt = 2.0A / 1μF
= 2 x 106 V/s
The rate of change in potential difference across the capacitor is, 2 x 106 V/s
Example 2: A parallel plate capacitor with plate area A and separation between the plates d, is charged by a constant current I. Consider a plane surface of area A/4 parallel to the plates and drawn between the plates. What is the displacement current through this area?
Solution:
Electric field between the plates of Capacitor
E= q/Aε0 = It / Aε0
Electric flux through area A/4 is,
φE = (A/4)E = It / 4ε0
Then displacement current is,
ID = ε0 (dφE / dt)
= ε0 d/dt (It / 4ε0)
= I/4
Hence, the displacement current through the required area is I/4.
Example 3: A parallel plate capacitor with circular plates of radius (R) is being charged. At the instant, the displacement current in the region between the plates enclosed between R/2 and R is given by
Solution:
Displacement Current is given by
I = ε0 (dφE / dt)
= ε0 A(dE / dt) (Since, φ=A.E)
= A (d/dt) (q/Ao)
= (A/Ao) i (Since, dq/dt = i)
Now, A = π(R/2)2, Ao = πR2
= π(R/2)2 / πR2
I = 1/4 i
Thus, the required displacement current is 1/4 i, where i is the conduction current.
Example 4: A coil that has 700 turns develops an average induced voltage of 50 V. What must be the change in the magnetic flux that occur to produce such a voltage if the time interval for this change is 0.7 seconds?
Solution:
Given:
Number of Turn (N) = 700
Induced Voltage (e) = 50 V
Time Interval (dt) = 0.7 s
By using Faraday’s Law,
e = N (dφ/dt)
Therefore, Change in flux (dφ) is,
dφ = e×dt / N
= 50×0.7 / 700
dφ = 0.05 Wb
Example 5: The magnetic flux linked with a coil having 250 turns is changed from 1.4 Wb to 2 Wb in 0.45 seconds. Calculate the induced emf in the coil.
Solution:
Given:
Number or Turns (N) = 250
Initial Flux (φ1) = 1.4 Wb
Final flux (φ2) = 2 Wb
Therefore, change in flux (dφ) can be given by,
dφ = φ2 – φ1 = 2 – 1.4 = 0.6 Wb
Time Interval (dt) = 0.45 s
According to Faraday’s Law,
Induced Emf (e) = N (dφ/dt)
e = 250 × (0.6 / 0.45)
e = 333.33 V
Example 6: A 0.20 m wide and 0.60 m long rectangular loop of wire is oriented perpendicular to a uniform magnetic field of 0.30 T. What is the magnetic flux through the loop?
Solution:
Given:
Length of Rectangular Loop (L) = 0.60 m
Breadth of Rectangular Loop (B) = 0.20 m
Area of Rectangular Loop (A) = 0.60 x 0.20 = 0.12 m2
Magnetic Field (B) = 0.30 T
We know that,
Magnetic Flux (φ) = BA
φ = 0.3 × 0.12
φ = 0.036 Wb
FAQs on Displacement Current
Q1: What is Displacement Current?
Answer:
Displacement current is the current in the insulated region of the charged capcitor due to the changing electric flux. It is a property of Maxwell’s Equation.
For a charged capacitor, the electric field between the plates is given by,
E = Q / ε0 A
Q = ε0 φE
Displacement Current is given by,
id = dQ/dt
id = ε0 (dφE /dt)
Q2: What is the SI unit of Displacement Current?
Answer:
The SI unit of Displacement Current is the same as the SI unit of Conduction current, i.e. Ampere (A)
Q3: How does the Displacement Current is produced?
Answer:
Displacement current is produced by the varying electromotive force and the time-varying electric field also produces the displacement current.
Q4: What is the Expression for the Displacement Current?
Answer:
The displacement current expression is,
ID = JDS = S(∂D/∂t)
where,
- S is the area of Capacitor Plate
- ID is the Displacement Current
- JD is the Displacement Current Density.
- D is related to Electric Field E as,
D = εE
- ε is the Permittivity of material between plates
Q5: State Ampere-Maxwell law
Answer:
Ampere-Maxwell law states that,
“The line integral of magnetic field around a closed loop is equal to μ0 times the sum of the conduction current and displacement current flowing therough the closed loop.”
Q6: What are the Uses of Displacement Current?
Answer:
Various uses of the displacement current are,
- Electromagnetic waves like radio waves, light waves, etc propagate through empty space using displacement current.
- Moving and changing electric field produces the displacement current.
- It helps us to explain Maxwell’s Equation.
Electromagnetic Waves
A wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities that is commonly described by a wave equation in physics, mathematics, and related subjects. Electromagnetic waves are a mix of electric and magnetic field waves produced by moving charges. The origin of all electromagnetic waves is a charged particle. This charged particle generates an electric field (which can exert a force on other nearby charged particles). When a charged particle accelerates as part of an oscillatory motion (as predicted by Maxwell’s equations), it causes ripples, or oscillations, in its electric field, as well as a magnetic field. Let’s take a closer look. The concept of electromagnetic waves!
What are Electromagnetic Waves?
Electromagnetic (EM) waves are waves that are related to both electricity and magnetism. These waves travel over space and are made up of time-varying electric and magnetic fields.
When electric and magnetic fields interact and change over time, electromagnetic waves are produced. These waves, which are linked to electricity and magnetism, would almost certainly travel beyond space.
The electromagnetic equations are derived using Maxwell’s equations. These EM waves, according to Maxwell, have a wide range of unique properties that can be applied to a variety of purposes. Electromagnetic waves are the connected temporally changing electric and magnetic fields that flow through space.
The magnetic field varies with time and gives rise to the electric field; the electric field changes with time and gives rise to the magnetic field again, and so on. When time-varying electric and magnetic fields are coupled and propagate together in space, electromagnetic waves are formed.

Electromagnetic Wave
The magnetic field, like the electric field, is a sine wave, except it goes in the opposite direction. Both of these fields (Electric and magnetic) generate electromagnetic fields. When the electric field is along the x-axis and the magnetic field is along the y-axis, the wave propagates on the z-axis. The propagation direction of waves and the electric and magnetic fields are perpendicular to each other.
Formation of Electromagnetic waves
In general, a charged particle generates an electric field. Other charged particles are pushed by this electric field. Negative charges accelerate in the opposite direction of the field, while positive charges accelerate in the field’s direction. The magnetic field is created by a travelling charged particle. Other moving particles are pushed by this magnetic field. Because the force acting on these charges is always perpendicular to their motion, it only influences the velocity’s direction, not its speed.
As a result, the electromagnetic field is created by an accelerating charged particle. Electric and magnetic fields travelling at the speed of light c through open space are referred to as electromagnetic waves. A charged particle is considered to be accelerating when it oscillates about an equilibrium place. The charged particle produces an electromagnetic wave of frequency f if its oscillation frequency is f. This wave’s wavelength λ can be determined using the formula λ = c/f. Electromagnetic waves are a sort of space-based energy transfer.
Sources of Electromagnetic Wave (EM)
- Electromagnetic waves are created when electrically charged particles vibrate. The vibration of the electric field associated with the speeding charge produces an oscillating magnetic field. These vibrating electric and magnetic fields produce electromagnetic waves.
- When the charge is at rest, the electric field associated with it is also static. As a result, because the electric field does not change with time, no EM waves are generated.
- A charge travelling at uniform velocity has no acceleration. Because the change in electric field with time is also constant, no electromagnetic waves would be generated. This illustrates that the only way to make EM waves is to accelerate charges.
- Consider the instance of an oscillating charge particle. It has an oscillating electric field that creates an oscillating magnetic field. After then, the oscillating magnetic field generates an oscillating electric field, and so on.
- The propagation of the wave = the regeneration of electric and magnetic fields.
- All of these events are contained in an electromagnetic wave. It’s also worth noting that the frequency of an EM wave is always equal to that of the oscillating particle that produces it.
Nature of Electromagnetic waves
- Transverse waves are Electromagnetic waves. The disturbance or displacement in the medium caused by transverse waves is perpendicular to the wave’s propagation direction. In such a wave, the medium particles travel in a path perpendicular to the wave’s propagation direction.
- The electric and magnetic fields will be perpendicular to an EM wave propagating along the x-axis. When wave propagation is parallel to the x-axis, the electric field is parallel to the y-axis, and the magnetic field is parallel to the z-axis.
- In nature, Electromagnetic waves are clearly transverse waves. The electric field of an EM wave is now provided by,
Ey = E0sin(kx-ωt )
where, Ey is the x-axis represents wave propagation, while the y-axis represents the electric field.
- The following formula is used to compute the wavenumber-
k = (2π/ωt)
- The magnetic field of an electromagnetic wave is created by,
Bz = B0sin( kx-ωt )
where, Bz is the electric field is along the z-axis, while the wave propagation direction is x.
B0 = (E0/c)
Here, we do some electromagnetic wave observations. In free space or vacuum, they’re self-sustaining electric and magnetic field oscillations. The electric and magnetic field vibrations are unlike any other waves we’ve looked at so far in that there is no material medium involved. Longitudinal compression and rarefaction waves are compressions and rarefaction waves in the air. A rigid, shear-resistant solid can also propagate transverse elastic (sound) waves.
Energy of Electromagnetic waves
- EM waves carry energy with them as they move. As a result of this feature, they have a wide range of uses in our daily lives. The energy of an EM wave is carried in part by an electric field and partly by a magnetic field.
- The total energy stored per unit volume in an EM wave is calculated as,
ET = Per unit volume electric field energy is stored + stored magnetic field energy per unit volume
ET = (1/2)(E2ε0) + (1/2)(B2μ0)
- Experimentally, it has been discovered that,
Speed of an EM wave = Speed of light
ET = (1/2)(E2ε0) + (1/2)(E2/c2μ0)
- Maxwell’s equations-
ET = (1/2)(E2ε0) + (1/2)(E2μ0ε0)
ET = E2ε0
Mathematical Representation of Electromagnetic Wave
It’s a plane we’re talking about. In the x-direction, the shape of an electromagnetic wave is
E(x , t) = Emax cos(kx – ωt + φ)
B(x , t) = Bmax cos(kx – ωt + φ)
where,
- E = electric field vector in an electromagnetic wave,
- B = magnetic field vector in an electromagnetic wave.
Maxwell was the first to envision electromagnetic radiations, while Hertz was the first to experimentally confirm the presence of an electromagnetic wave. The propagation direction of an electromagnetic wave is determined by the vector cross product of the electric and magnetic fields. It’s written like this:
Characteristics of EM waves
- The velocity of EM waves in open space or vacuum is a fundamental constant. In experiments, the velocity of EM waves was discovered to be the same as the speed of light. (c = 3 × 108 m/s). c is a basic constant defined as follows :
c = 1/√μ0ε0
- EM waves require time-varying electric and magnetic fields to propagate. Electromagnetic waves convey both energy and velocity.
- ET=E2ε0 is the total energy stored per unit volume in EM waves (Partly carried by an electric field and partly by magnetic field). This is a vital element for EM waves practical applications since they carry both energy and momentum.
- EM waves are used in communication, such as in cell phone speech communication.
- Electromagnetic waves (EM waves) apply pressure. Because they carry energy and momentum, they exert pressure. The force exerted by electromagnetic waves is known as radiation pressure.
- The form of sunlight that we receive from the sun, for example, is visible light rays. These light beams are included in EM waves. Our hand will become warm and sweaty if we leave them in the sun for a long time. Because sunlight is transmitted in the form of energy-carrying electromagnetic waves (EM waves), this occurs.
- Assume that the total energy transferred to the hand is equal to E. Momentum = (E/c) Because c is so huge, the momentum appears to be little. The pressure is also low because the momentum is so low. Because of this, our hands are not affected by the sun’s pressure.
Applications of Electromagnetic Waves
- These waves assist the pilot in navigating the aircraft and accomplishing a smooth take-off and landing. They’re also used to figure out how fast planes are flying.
- Radio and television broadcasting signals are transmitted via electromagnetic waves.
- In the medical field, these waves can be used in a variety of ways. X-rays and laser eye surgery, for example.
- They are utilized in electronic equipment like television remote controls, remote vehicles, LED televisions, microwave ovens, and so on.
- Electromagnetic waves can be used to determine the speed of passing cars.
Sample Questions
Question 1: In free space, a planar electromagnetic wave with a frequency of 44 MHz moves in the x-direction. E = 7.3 V/m at a specific point in space and time. At this moment, what is B?
Answer:
Given : E = 7.3 V/m, c = 3 × 108 m/s
We have,
B = E/c
∴ B = 7.3 / 3 × 108
∴ B = 2.433 × 108 T
We may determine the direction by noting that E is along the y-axis and the wave propagates along the x-axis. As a result, B should be perpendicular to both the x- and y-axes. E × B should be along the x-axis, according to vector algebra. B is in the z-direction because-
(+
) × (+
) =
.
Thus,
Question 2: The magnetic field in a plane electromagnetic wave is given by By =(2 × 10-7)T sin (0.5 × 103x + 1.5 × 1011t). What are the wave’s wavelength and frequency?
Answer:
Comparing the given equation with
By = B0 sin[2π(x/λ + t/T)]
We have,
λ = (2π/0.5×103) m = 1.26 cm.
And 1/T = ν = 1.5 × 1011)/2π = 23.9 GHz.
Question 3: At normal incidence, light with an energy flow of 18 W/cm2 falls on a non-reflecting surface. Find the average force applied on the surface over a 30-minute period if the surface has an area of 20 cm2.
Answer:
The total amount of energy that falls on the surface is
U = (18 W/cm2) × (20 cm2) × (30 × 60 s)
∴ U = 6.48 × 105 J
As a result, the total delivered momentum (for complete absorption) is
p = U/c
∴ p = 6.48 × 105 J / 3 × 108 m/s
∴ p = 2.16 × 10–3 kg m/s
The surface is subjected to an average force of
F = p/t
∴ F = 2.16 × 10-3 / 0.18 × 104
∴ F = 1.2 × 10-6 N
Question 4: Write four applications of electromagnetic waves.
Answer:
Applications of electromagnetic waves :
- We can see everything around us thanks to electromagnetic radiation.
- These waves assist the pilot in navigating the aircraft and accomplishing a smooth take-off and landing. They’re also used to figure out how fast planes are flying.
- In the medical field, these waves can be used in a variety of ways. X-rays and laser eye surgery, for example.
- Radio and television broadcasting signals are transmitted via electromagnetic waves.
Question 5: Explain the formation of electromagnetic waves.
Answer:
In general, a charged particle generates an electric field. Other charged particles are pushed by this electric field. Negative charges accelerate in the opposite direction of the field, while positive charges accelerate in the field’s direction.
The magnetic field is created by a travelling charged particle. Other moving particles are pushed by this magnetic field. Because the force acting on these charges is always perpendicular to their motion, it only influences the velocity’s direction, not its speed.
As a result, the electromagnetic field is created by an accelerating charged particle. Electric and magnetic fields travelling at the speed of light c through open space are referred to as electromagnetic waves. A charged particle is considered to be accelerating when it oscillates about an equilibrium place. The charged particle produces an electromagnetic wave of frequency f if its oscillation frequency is f. This wave’s wavelength λ can be determined using the formula λ = c/f. Electromagnetic waves are a sort of space-based energy transfer.
Electromagnetic Spectrum
Electromagnetic Spectrum: The sun is our planet’s principal source of energy, and its energy travels in the form of electromagnetic radiation. Electromagnetic energy moves across space at the speed of light in the form of waves of electric and magnetic fields with a range of frequencies or wavelengths.
Electromagnetic radiation is a common occurrence in our daily lives. All electromagnetic waves, from visible light, that our eyes can detect to microwave radiation that heats our meals or radio waves that power our radios, X-rays that enable doctors to identify any injury in our bones, or UV radiation emitted by a hot surface, are EM waves.
In this article, we have provided all types of electromagnetic radiation in the Electromagnetic Spectrum, their properties, diagrams, and applications of Electromagnetic Spectrum.
Table of Content
- What is an Electromagnetic Spectrum?
- Electromagnetic Waves
- Representation of Electromagnetic Waves
- Electromagnetic Spectrum
- Terms Related to Electromagnetic Waves
- Electromagnetic Waves in Electromagnetic Spectrum
- Electromagnetic Spectrum Wavelength and Frequency Table
- Spectroscopy
- Applications / Uses of Electromagnetic Spectrum
- Electromagnetic Spectrum – Sample Questions
What is an Electromagnetic Spectrum?
Consider the electromagnetic spectrum as a wide cosmic highway that facilitates the movement of various kinds of light. There is a vast spectrum of energy waves present in this, ranging from extremely short waves like X-rays to long, languid waves like radio broadcasts. This spectrum extends beyond the light that our eyes can detect.
The tiny portion of light that we can see, known as visible light, which includes every color in the rainbow, is located exactly in the middle of this enormous spectrum. But there’s so much more to it than that.
On one extreme are the incredibly small and intense gamma and X-rays, which are employed in medicine to view the body and can penetrate through solid objects. The radio waves, on the other hand, are like the long, slow waves that carry your favorite radio station’s music through the air to your radio.
Electromagnetic Spectrum Definition
The electromagnetic (EM) spectrum is the range of all types of electromagnetic radiation, which is energy that disperses and expands as it travels. This includes everything from the visible light emitted by a household lamp to the radio waves broadcast by radio stations, illustrating the diverse forms of electromagnetic radiation.
Electromagnetic Waves
Waves created by the interaction of vibrating electric and magnetic fields are known as electromagnetic waves. An oscillating electric and magnetic field makes up EM waves.
A charged particle, in general, produces an electric field. This electric field exerts a push on other charged particles. Positive charges accelerate in the field’s direction, whereas negative charges accelerate in the opposite direction of the field. A traveling charged particle creates a magnetic field.
This magnetic field exerts a push on other moving particles. Because the force acting on these charges is always perpendicular to their movement, it only affects the direction of the velocity, not the speed. As a result, a speeding charged particle generates an electromagnetic field. Electromagnetic waves are nothing more than electric and magnetic fields traveling at the speed of light c through open space.
When a charged particle oscillates about an equilibrium location, it is said to be accelerating. If the charged particle’s oscillation frequency is f, it creates an electromagnetic wave of frequency f. The wavelength of this wave may be calculated using the formula:
λ = c/f
Electromagnetic waves are a type of energy transfer that occurs in space.
Representation of Electromagnetic Waves
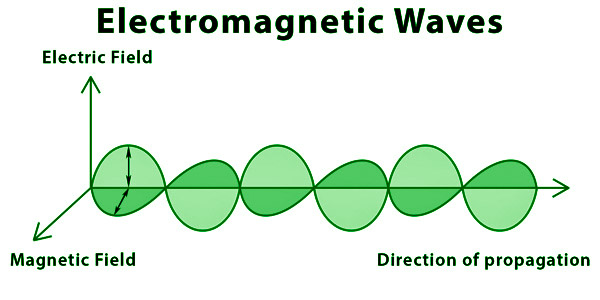
Electromagnetic Spectrum
The electromagnetic spectrum is a collection of frequencies, wavelengths, and photon energies of electromagnetic waves spanning from 1Hz to 1025Hz, equivalent to wavelengths ranging from a few hundred kilometres to a size smaller than the size of an atomic nucleus.
The electromagnetic spectrum can thus be described as the range of all types of electromagnetic radiation in basic terms. In a vacuum, all electromagnetic waves travel at the same speed as light. For different forms of electromagnetic waves, however, the wavelengths, frequencies, and photon energy will vary.
Electromagnetic Spectrum Diagram
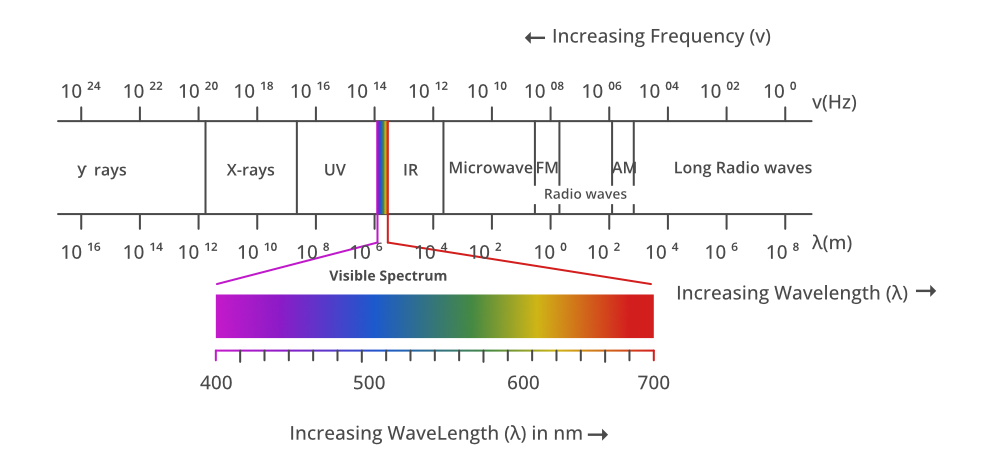
Terms Related to Electromagnetic Waves
The frequency (f), wavelength (λ), energy (E) of an electromagnetic wave are related to each other as:
λ=c/f
f=E/h
E=hc/λ
where
- c=3×108m/s represents the speed of light in a vacuum
- h=6.626×10–34J.s represents Planck’s constant.
Electromagnetic Waves in Electromagnetic Spectrum
Radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, gamma rays, and cosmic rays make up the full range (electromagnetic spectrum) in decreasing order of frequency and rising order of wavelength.
Radio Waves
- The rapid travel of charged particles across conducting wires causes these waves.
- Radio, television, and telecom signals are transmitted through them.
- These waves have a frequency range of around 3kHz to 300MHz.
- In the ultrahigh-frequency (UHF) band, cellular phones employ radio waves to convey voice communication.
- Radio picks up radio waves that are broadcast by radio stations. Radio waves can be emitted by gases and stars in space. The majority of radio waves are used for TV and mobile communication.
Microwaves
- Microwaves are a type of electromagnetic radiation that has a frequency of a few gigahertz (GHz).
- Klystrons, magnetrons, and Gunn diodes are unique vacuum tubes that produce them.
- Microwaves are commonly utilised in aviation navigation due to their short wavelengths.
- These rays are employed in microwaves, which aid in the heating of meals in homes and offices. It’s also used by astronomers to figure out and understand the structure of surrounding galaxies and stars.
Infrared Rays
- Infrared waves are produced by hot bodies and molecules and are thus referred to as heatwaves.
- Infrared rays are near the low-frequency or long-wavelength end of the visible light spectrum.
- The greenhouse effect caused by these rays is critical for maintaining global warming and average temperatures.
- Greenhouse gases such as carbon dioxide and water vapour trap these radiations in the earth’s atmosphere.
- Night vision goggles make use of these radiations. Infrared light generated by objects in the dark can be read and captured by these devices. Infrared light is used to trace interstellar dust in space. Infrared radiation is emitted by electronic devices and is commonly employed in remote switches for a variety of household gadgets.
Visible Rays
- Visible rays are electromagnetic waves that can be seen with the naked eye. They are the most common type of electromagnetic waves.
- These can be found in the frequency range of 4×1014Hz–7×1014Hz or the wavelength range of 400nm–700nm.
- The visible light rays reflected or released from the objects around us assist us in seeing the world, and the range of visible radiation is different for different creatures.
- Devices that emit light in the visible area of the electromagnetic spectrum include bulbs, lamps, candles, LEDs, tube lights, and so on.
Ultraviolet Rays
- Although the sun is the primary source of ultraviolet radiation on Earth, the ozone layer absorbs the majority of UV energy before it reaches the atmosphere.
- UV radiation has a wavelength of 400nm–1nm.
- These radiations are emitted by special lamps and extremely hot bodies, and in big numbers, they can cause significant injury to humans. It tans the skin and creates burns.
- Because these radiations may be focused on tiny beams, they are used in high precision applications such as LASIK or laser-based eye surgery.
- UV lamps are used in water purifiers to eliminate microorganisms that may be present in the water.
- When working with UV welding arcs, welders use special goggles to protect their eyes.
X-Rays
- This electromagnetic radiation is found outside of the ultraviolet (UV) region of the electromagnetic spectrum and is extremely valuable in the medical field.
- The wavelength range of X-ray radiation is 1nm–10–3nm.
- By blasting a metal target with high-energy electrons, X-rays can be produced.
- X-rays are a diagnostic technique in medicine that can be quite helpful in the treatment of some types of cancer. To find the source of the problem, a doctor utilises an x-ray scanner to scan our bones or teeth. Overexposure to x-rays can cause harm or death to the organism’s healthy tissues. As a result, extreme caution must be exercised when dealing with x-rays.
- At the airport checkpoint, security agents utilise it to search through passengers’ luggage. X-rays are also emitted by the universe’s heated gases.
Gamma-Rays
- The universe is the largest gamma-ray generator.
- These rays are in the electromagnetic spectrum‘s higher frequency region.
- Gamma rays have wavelengths ranging from 10–12m to 10–14m.
- Radioactive nuclei release high-frequency radiations, which are also created during nuclear processes.
- Gamma rays have a wide range of medical applications, including the destruction of cancerous cells. Gamma-ray imaging is a technique used by doctors to examine the insides of patients’ bodies.
Electromagnetic Spectrum Wavelength and Frequency Table
The table provided below provides the Electromagnetic Spectrum Wavelength and Frequency of all types of electromagnetic radiations:
Types of Radiation | Frequency range (Hz) | Wavelength Range |
Gamma-rays | 1020-1024 | <10-12 m |
X-rays | 1017-1020 | 1 nm – 1 pm |
Ultraviolet rays | 1015-1017 | 400 nm – 1 nm |
Visible rays | 4 x 1014 – 7.5 x 1014 | 750 nm – 400 nm |
Near-infrared | 1 x 1014 – 4 x 1014 | 2.5 μm – 750 nm |
Infrared rays | 1013 – 1014 | 25 μm – 2.5 μm |
Microwaves | 3 x 1011 – 1013 | 11 mm – 25 μm |
Radio waves | < 3x 1011 | >1 mm |
Also Read:
Spectroscopy
In terms of wavelength or frequency, spectroscopy is a method for determining the emission and absorption of light and other radiation as it interacts with matter.
As a ray of light passes through matter, it is scattered. It interacts with atoms and molecules of the given substance, and these atoms interact with light waves of similar frequencies based on their resonance frequencies.
When light rays collide with an atom in an excited state, certain distinctive frequencies are released, resulting in a line spectrum. This line spectrum is made up of a collection of emission lines that isn’t continuous.
The wavelengths of the light produced are separated. When light with continuous wavelengths is passed through a low-density material, an absorption spectrum is created. Atoms and molecules with characteristic frequencies similar to light waves will be absorbed, resulting in a continuous spectrum with a few lines missing.
Applications / Uses of Electromagnetic Spectrum
The presence of the full electromagnetic spectrum was originally demonstrated by Maxwell. His mathematics suggested that electromagnetic radiation may have an endless number of frequencies. The electromagnetic spectrum is a frequency and wavelength-based organization of various radiations.
The following are some examples of EM-spectrum applications:
- Hertz was the first to discover radio waves and microwaves. Wireless television and radio, as well as mobile communication, arose as a result of these waves.
- Ultraviolet radiation is useful for the ionisation of atoms, which aids in the initiation of numerous chemical reactions.
- The gamma rays were discovered by Paul Villard. These are employed in the development of nuclear medicine and ionization experiments.
- X-rays were invented by Roentgen. These are used to discover problems with the bones and teeth, as well as abnormalities.
- The visible light portion of the electromagnetic spectrum allows us to see the world around us. This part of the electromagnetic spectrum aids in the perception of all objects, including colours.
People Also View:
Electromagnetic Spectrum – Sample Questions
Question 1: What are electromagnetic waves?
Answer:
Electromagnetic waves are vibrations made up of perpendicularly oscillating electric and magnetic fields.
Question 2: What are the frequency and wavelength of an EM wave of energy 6.626 x 10-19 J?
Answer:
Frequency(f) = E/h
= 1015 Hz.
Wavelength(λ) = c/f
= 3 x 108 / 1015
= 3 x 107 m
Question 3: What is Spectroscope?
Answer:
Spectroscopy is the study of how light and other electromagnetic radiation are emitted and absorbed by matter based on the wavelength or frequency of the energy.
Conclusion of Electromagnetic Spectrum
The electromagnetic spectrum is like an invisible rainbow of energy, with each “color” representing a different type of wave traveling through space. From long radio waves to short gamma rays, these waves carry energy at the speed of light, produced by electric and magnetic forces. They impact everything around us: from the sun’s warmth and X-rays to microwaves, UV rays, and radio waves. Each wave has a unique wavelength and frequency, connecting cosmic energy to our everyday technologies.
Electromagnetic Spectrum – FAQs
What is the electromagnetic spectrum?
The electromagnetic spectrum is a range of all types of electromagnetic radiation, including visible light, radio waves, and X-rays, organized by their wavelengths.
What are the 7 electromagnetic waves?
The seven electromagnetic waves are radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays.
What is electromagnetic spectrum and its functions?
The electromagnetic spectrum is a range of all types of electromagnetic radiation, organized by wavelength. Its functions include transmitting information (like radio waves), heating (like microwaves), and imaging (like X-rays).
What are the Practical Applications of Electromagnetic Waves?
Practical applications of electromagnetic waves include communication (e.g., radio and Wi-Fi), cooking (e.g., microwaves), medical imaging (e.g., X-rays), and more.
Which electromagnetic spectrum has the highest wavelength?
Radio waves in the electromagnetic spectrum have the highest wavelength.
Which part of the electromagnetic spectrum has the highest frequency?
Gamma rays in the electromagnetic spectrum have the highest frequency.
Which part of the electromagnetic spectrum carries the least energy?
Radio waves in the electromagnetic spectrum carry the least energy.
Where in the electromagnetic spectrum is visible light?
Visible light is in the middle of the electromagnetic spectrum.
What is the increasing frequency of electromagnetic spectrum?
The electromagnetic spectrum increases in frequency from radio waves to microwaves, then infrared, visible light, ultraviolet, X-rays, and finally, gamma rays, with gamma rays having the highest frequency.
What is emw spectrum?
The electromagnetic spectrum ranges from low-frequency radio waves to high-frequency gamma rays, including microwaves, infrared, visible light, ultraviolet, and X-rays, each with unique properties and uses.

0 Comments