CHAPTER 13 NUCLEI

 

CHAPTER 13 NUCLEI

Structure of Nucleus

Last Updated : 25 Feb, 2024

The nucleus of an atom consists of two types of particles, positively charged particles called protons and neutrally charged particles called neutrons. Protons + Neutrons in an atom represent the nucleus of an atom. The nucleus of an atom is represented by ZXA, where X is the nucleus of an atom, Z is the atomic number and A is the mass number.

Terms Related to the Nucleus of an Atom

• Nucleons: Protons and neutrons which are present in the nuclei of atoms are collectively known as nucleons.
• Atomic Number: The number of protons in the nucleus is called the atomic number of the element. It is denoted by Z.
• Mass Number: The total number of protons and neutrons (collectively known as nucleons) present in a nucleus is called the mass number of the element. It is denoted by A.
• Nuclear Mass:  The total mass of the protons and neutrons present in a nucleus is called nuclear mass.

Note: Few important points to remember regarding the nucleus are:

• Number of protons in an atom = Number of electrons in an atom = Z
• Number of nucleons in an atom = A
• Number of neutrons in an atom N = A – Z
• A proton has a positive charge Qp= 1.6×10-19 C and mass mp = 1.6726×10-27kg  
• A neutron has no charge and its mass mn = 1.6749×10-27kg  
• No electrons are present inside the nucleus.

Types of Nuclei

Various types of Nuclei are discussed below:

• Isotopes: These are nuclei of the same element having the same Z but different A.  Ex– 8O16, 8O17, 8O18
• Isotones: These are nuclei of different elements having the same N but different A. Ex– 6C137 and 7N147
• Isobars: These are nuclei of different elements having the same A but different N and Z. Ex– 6C14 and 7N14
• Mirror Nuclei: These are nuclei with the same A but in which neutron and proton numbers are interchanged. Ex– 4Be73(Z= 4, N=3) and 3Li74(Z=3, N=4)
• Isomer Nuclei: These are nuclei with the same A and same Z but differ in their nuclear energy states. They have different lifetimes and internal structures. These nuclei have different radioactive properties. Ex– Co60 and Co60*

Size of the Nucleus

Rutherford assumed the distance of the closest approach as a measure of the size of an atomic nucleus. Assuming, the nuclei are spherical, the relation between the radius of the nucleus and the mass number is given by:

R = R0A1/3 

where, 
R0 is constant
For electrons R0 = 1.25×10-15m = 1.25 fermi(fm)

The Radius R of a nucleus is proportional to the cube root of its mass number. 

Density of Nucleus

The nuclear density is independent of mass number A. The nuclear density is nearly constant and is equal to

ρ = (3m)/(4πR0 3) = 2.04×1017 kg/m3

where m is the mass of a nucleus

Atomic Mass Unit (u or amu)

One atomic mass unit is defined as (1/12)th of the actual mass of a carbon-12 atom. It is denoted by amu or u.

1 amu = (1/12)× Mass of carbon-12 atom

           = (1/12) × 1.992678×10-26 kg

1 amu = 1.660565×10-27 kg

Electron Volt

It is defined as the energy acquired by an electron when it is accelerated through a potential difference of 1 volt and is denoted by eV.

1 eV = 1.602×10-19J

Relation between amu and MeV: 

1 amu = 931 MeV

Nuclear Forces

The strong forces of attraction which firmly hold the nucleons in the small nucleus and account for the stability of the nucleus are called nuclear forces.

Characteristics of Nuclear Force

Some important characteristics of Nuclear Forces are:

• Nuclear force is a short-range force.
• Nuclear forces are the strongest force in nature.
• Nuclear forces are charge-independent.
• Nuclear forces are spin-dependent.
• Nuclear forces show saturation property.
• Nuclear forces are non-central forces.
• Nuclear forces are exchange forces.

Mass Defect

The mass of the nucleus is always less than the sum of the masses of nucleons composing the nucleus. The difference between the rest mass of the nucleus and the sum of the rest masses of nucleons constituting the nucleus is known as mass defect.

△m = [Zmp +(A-Z)mn] – M(ZXA)

where,
mp = mass of protons
Z = Atomic number
A = Mass number

Binding Energy

The energy required to break a nucleus into its constituent nucleons and place them at an infinite distance is called binding energy.

BE = (△m) c2 = c2 [Zmp +(A-Z)mn– M(ZXA)]

where,
mp = mass of protons
Z = Atomic number
A = Mass number
c = speed of light

Rest Mass of Protons + Rest Mass of Neutrons = Rest Mass of Nucleus + BE

Binding Energy per Nucleon

The binding energy per nucleon of a nucleus is the average energy required to extract a nucleon from the nucleus.

Binding energy per nucleon $\bar{B}=\frac{\text{Total binding energy}}{\text{Total number of nucleons}}=\frac{BE}{A}=\frac{\mathrm{△}m{c}^2}{A}$

Solved Examples of Structure of Nucleus

Example 1: Compare the radii of two nuclei with mass numbers 1 and 27 respectively.

Solution:

Radius of nucleus R = R0A1/3

 $\frac{R_1}{R_2}=(\frac{A_1}{A_2}{)}^{1\mathrm{/}3}$

 R1/R2 = (1/27)1/3

            = 1/3

Example 2: What is the nuclear radius of 125Fe if that of 27Al is 3.6 fermi?

Solution:

Nuclear radius, R = R0A1/3 ⇒ R∝A1/3

For Al, A = 27, RAl = 3.6 fermi, 

For Fe A = 125

$\frac{R_{Fe}}{R_{Al}}=(\frac{A_{Fe}}{A_{Al}}{)}^{1\mathrm{/}3}$

RFe/RAl = (125/27)1/3

RFe = (5/3)RAl 

       = (5/3) ×3.6 fermi

RFe = 6 fermi

Example 3: A neutron breaks into a proton and electron. Calculate the energy produced in this reaction in MeV. Mass of an electron = 9.1 ×10-31 kg, Mass of proton = 1.6725×10-27 kg, Mass of neutron 1.6747×10-27 kg. Speed of light = 3×108 ms-1.

Solution: 

Mass defect (△)m = Mass of neutron – (mass of proton + mass of electron)

△m = [(1.6747×10-27) – (1.6725×10-27 + 9.1 ×10-31)]

△m = 0.0013×10-27 kg

Energy released Q = △mc2

Q = (0.0013×10-27) × (3×108)2

    = 1.17×10-13 J

Q = (1.173×10-13) / (1.6×10-19)

    = 0.73×106 eV

Q = 0.73 MeV

Example 4: Find the binding energy of 126C. Also, find the binding energy per nucleon. Given mass of 11H = 1.0078 u, 10n =1.0087 u, 126C = 12.00004u.

Solution: 

One atom of 126C consists of 6 protons, 6 electrons, and 6 neutrons. The mass of the uncombined protons and electrons is the same as that of six 11H atoms.

Mass of six 11H atoms = 6×1.0078 = 6.0468 u

Mass of six neutrons = 6 × 1.0087 = 6.0522 u

Total mass of particles = 6.0468 +6.0522 
                                    = 12.0990 u

Mass of 126C atom = 12.00004

Mass defect = 12.0990 – 12.00004 
                   = 0.0990 

Binding energy = 931 × (0.099) 
                        = 92 MeV

Binding energy per nucleon = 92/12
                                            = 7.66 MeV

FAQs on Structure of Nucleus

Question 1: What are nucleons?

Answer: 

Protons and neutrons which are present in the nuclei of atoms are collectively known as nucleons.

Question 2: What is a mass number?

Answer: 

The total number of protons and neutrons (collectively known as nucleons) present in a nucleus is called the mass number of the element. It is denoted by A.

Question 3: What do you mean by atomic mass unit (amu)?

Answer: 

One atomic mass unit is defined as (1/12)th of the actual mass of a carbon-12 atom. It is denoted by amu or u. 1 amu = 1.660565×10-27 kg

Question 4: State the relation between amu and MeV.

Answer:

1 amu = 931 MeV

Question 5: How to find the number of neutrons in an atom?

Answer:

Number of neutrons in an atom (N) = Mass number (A) – Number of protons in an atom (Z)

Question 6: State the relation between the radius of a nucleus and mass number.

Answer:

R = R0A1/3 

where, 
R0 is constant
For electrons R0 = 1.25×10-15m = 1.25 fermi(fm)

Related Resource

• Molecule and Compound
• Isotopes and Isobars
• Density of Gas

 

Size of The Nucleus – Rutherford Gold Foil Experiment

Last Updated : 25 Feb, 2024

Physics requires an understanding of matter’s underlying structure. Without the Rutherford gold foil experiment, it would be impossible to determine the size of the nucleus, which is the subject of this article. The Rutherford atom model was the first proper interpretation of the atom, and it served as the foundation for Bohr’s interpretation.

Rutherford demonstrated from his experiments that the radius of a nucleus is smaller than the radius of an atom by a factor of about 10 4 and the atomic nucleus is the central core of every atom. The nucleus contains enter a positive charge and more than 99.9 % of the mass of the atom, in other words, an atom is almost empty.

An atom consists of a central positively charged region called the nucleus which consists of positively charged particles called protons and neutral particles called neutrons.

Rutherford Gold Foil Experiment 

J.J Thompson in 1898, proposed a model of the atom which looked more or less like plum pudding are raisin pudding. He assumed an atom to be a spherical body in which electrons are unevenly distributed in a sphere having a positive charge which balances the electron’s charge. It is called the Plum Pudding model.

The mass of the atom is assumed to be uniformly distributed over the whole atom. It failed after rutherford’s α scattering experiment which proved the atom to be quite different. 

In this experiment Rutherford allows a narrow beam of α particles to fall on a very thin gold foil. This gold foil had a circular fluorescent Zinc sulphide screen around it. The α particles emitted by radioactive substances are dipositive Helium ions (He+2 ) having a mass of 4 units and 2 units of positive charge. A tiny flash of light was produced at the point where α particles truck.

Rutherford Gold Foil Experiment 

Observations of Rutherford Gold Foil Experiment:

• Most of the Alpha particles passed through the foil without any deflection.
• Few α particles were deflected by small angles.
• Very few Alpha particles (1 out of 20,000 particles) completely rebound. i.e. deflected at ∼180.

Conclusion of Rutherford Gold Foil Experiment:

• The presence of largely empty space in the atom.
• The positive charge is concentrated at a very small region and is not uniformly distributed in the whole atom (If not then a large number of α particles would have been deflected by experiencing the enormous repulsive force from the positive charge of the atom).
• The positively charged core is known as the nucleus.
• Based on the Alpha scattering experiment Rutherford gave the nuclear model of an atom

Features of Rutherford Gold Foil Experiment:

• In an atom, the mass and positive charge are centrally located in an extremely small region called the nucleus.
• The volume of the nucleus is negligible as compared to the total volume of the atom.
• Both protons and neutrons present in the nucleus are collectively called nucleons.
• Extranuclear part: the nucleus is surrounded by revolving electrons. electrons revolve with very high speed in circular paths called orbits, so as in counterbalance of the electrostatic force of attraction between protons and electrons.
• Rutherford’s model of atom resembles the solar system in which the nucleus plays the role of the sun and the electrons of revolving planets.
• The centrifugal force acting outwards balances the inward coulombic attraction by the nucleus. This stabilizes the electrons in their orbits.

A new model of the atom was required to explain these findings. The positive stuff was thought to be concentrated in a tiny but vast location dubbed the nucleus in the new concept. To complete this picture, electrons were thought to be rotating around the nucleus, preventing one atom from intruding on its neighbour’s space.

Size of Nucleus  

The first experimental determination of a size of a nucleus was made from the results of Rutherford scattering of α particles. Distance of closest approach was found to be read into 3 ×10-14 m for 7.7 MeV energetic α particles. This fact indicated that the size of the nucleus should be less than 3 ×10-14 m. For α particles having a kinetic energy of more than 7.7 MeV, the distance of the closest approach will be smaller. 

At K.E more than 5.5 MeV distance of closest approach will be smaller. At K.E more than 5.5 MeV, attractive nuclear forces start affecting the Coulomb’s repulsive force between α  particles and gold nucleus. The size of the nucleus can be measured by using fast electrons instead of α particles for the scattering experiment. The nuclear size was found to vary linearly with the mass number (A). Since the nucleus is supposed to be spherical, having radius R.

R = R0A1/3

where R0 = 1.2×10-15 m

Nuclear Density 

A nucleus’ density (ρ) is equal to its mass divided by its overall volume. Nucleons are the number of protons and neutrons in a nucleus, and their mass is A times the mass of the nucleon (A is the number of nucleons in the atom).

Nuclear density, ρ = mass of nucleus /volume of nucleus = (mass of proton or neutron)(mass number) / Volume of the nucleus.

Consider A nucleus with the mass number A and radius R.

The volume of nucleus = 4/3 πR3

But

R = R0A1/3  

where R0 is a constant.

The volume of nucleus=4/3 π R03A

Then     

ρ = (1.66×12-27)A/4/3 π R03A 

    = (1.66×10-27)/4/3π (1.2×10-15)3

 R0 = 1.2×10-15m

ρ = 3 ×1.66×10-27/4×3.14(1.2×10-15)3

   = 2.38×1017kg m-3

Thus nuclear density ρ is constant. That is independent of mass number for all nuclei. 

Note:

• Heavier nuclei are bigger in size than lighter nuclei.
• Nuclear density is independent of the mass number of an atom.
• Nuclear density (=1017 kgm-3)is about 1013 times the average density of earth (=104 kg m-3)

Sample Questions

Question 1: Calculate the radius of a nucleus of mass number 8.

Answer:

The radius of a nucleus is given by, 

R = R0A1/3

R0 =1.2×10-15 m;  A=8

R=1.2×10-15 ×(8)1/3

   =1.2 ×10-15 ×2 =2.4 ×10-15 m.

Question 2: What is the nuclear radius of 125Fe, if that of 27Al is 3.6 Fermi?

Answer:

Since, 

R = R0A1/3

RFe/RAl = (AFe/AAl)1/3

            = (125/27)1/3

      RFe = 5/3 RAl 

             = 5/3 × 3.6 

             = 6.0 Fermi 

Question 3: Find the mass density of the oxygen nucleus 8O16.

Answer:

Since, Volume, V = 4/3π R3 = 4/3 π (1.2×10-15)3 A

                           =1.16 ×10-43 m3

Mass of oxygen atoms (A =16) is approximately 16 u.

Therefore density is, 

ρ = m/V

   = 16 × 1.66 × 10-27 / 1.16 × 10-43

   = 2.3 × 1017 kg/m3.

Question 4: Find the ratio of nuclear radii of tungsten isotope 74W186 and iron isotope 26Fe56.

Answer:

Mass number of tungsten, A1 = 186

Nuclear radius of tungsten R1 = R0A11/3

Mass number of iron, A2 = 56

Nuclear radius of iron, R2 = R0A21/3

R1/R2 = (A1/A2)1/3

          = (186/56)1/3 

          = (3.32)1/3      

Or 

R1/R2 = 1.491

Taking log of equation (i) ,we get

log (R1/R2) = 1/3 log (3.32)

                  = 1/3(0.5211) = 0.1737

Taking antilog both sides,

R1/R2. = 1.491

Question 5: Given the mass of the iron nucleus as 55.85 u with A = 56. Find the nuclear density.

Answer:

M = 55 × 85 u

    = 55.85 × 1.67 × 10-27 kg

Volume, V = 4/3 π R3 = 4/3  (R0A1/3)3

                 = 4/3π R03 × A

Nuclear density = M/V = 3M/4π R03A

                                    = 3 × 55.85 (1.67×10-27) / 4 × 3.14(1.2 × 10-15)3 × 56

                                     = 2.29×1017 kg/m3 

 

Nuclear Binding Energy – Definition, Formula, Examples

Last Updated : 15 May, 2024

During the twentieth century, Albert Einstein, a well-known scientist, developed the revolutionary theory known as “the theory of relativity.” Mass and energy are interchangeable, according to the theory; mass can be turned into energy and vice versa. This additional dimension to physics benefited in resolving many unsolved problems and provided a platform for many new hypotheses. The presence of Nuclear Binding Energy is one of them. As a result, there is a comprehensive understanding of nuclear mass and inter-nuclei interactions.

The forces that bind nucleons together in an atomic nucleus are considerably stronger than the electrostatic forces that hold an electron to an atom. The relative diameters of the atomic nucleus and the atom (1015 and 1010 m, respectively) demonstrate this. As a result, the energy required to pry a nucleon from its nucleus is substantially more than that required to remove (or ionize) an electron from an atom. All nuclear reactions, in general, involve substantial amounts of energy per particle involved in the reaction. This has a wide range of applications.

Now, Let’s understand the concept of Binding Energy in depth!

What is Nuclear Binding Energy?

Nuclear binding energy is the amount of energy required to keep the protons and neutrons in an atom’s nucleus together. As a result of the energy required to maintain neutrons and protons together, the nucleus remains intact.

It can alternatively be described as the amount of energy required to separate the nucleons. Nuclear binding energy is a measure of how tightly nucleons are bonded to one another. This can be concluded if neutrons and protons are strongly or loosely connected to each other by determining their value. And this can be interpreted as:

• If the nuclear binding energy is large, it takes a lot of energy to separate the nucleons, indicating that the nucleus is very stable.
• If the nuclear binding energy is low, it takes less amount of energy to separate the nucleons, indicating that the nucleus isn’t completely stable.

Mass Defect and Binding Energy

An atom is made up of a nucleus in the centre and electrons orbiting around it in an orbital pattern. Protons and Neutrons combine to form nuclei, which are referred to as nucleons. As a result, we expect the nucleus’ mass to be equal to the sum of the individual masses of neutrons and protons. However, this is not the case. The nucleus’ overall mass (mnuc) is smaller than the sum of the individual masses of neutrons and protons that make it up. This disparity in mass is referred to as a mass defect.

Δm = Zmp+(A−Z)mn−mnuc

where,

Zmp is the total mass of the protons.

(A-Z)mn is the total mass of the neutrons.

mnuc is the mass of the nucleus.

The mass energy is equivalent, according to Einstein’s theory of relativity. That is, the total energy of a system is measured by its mass. E=mc2 is a well-known equation. As a result, the nucleus’ overall energy is smaller than the sum of the energies of individual protons and neutrons (nucleons). This means that when the nucleus breaks down into its constituent nucleons, some energy is released in the form of heat energy. (This is an exothermic process.) The energy emitted here is expressed mathematically as

E = (Δm)c2

Consider the case of a nucleus that has been broken. A specific quantity of energy is placed into the system to do this. Nuclear binding energy is the amount of energy necessary to do this. As a result, nuclear binding energy can be defined as, The minimum energy required to separate nucleons into its constituent protons and neutrons. and is given by-

Eb = (Δm)c2

Hence, the difference in the mass is converted into Nuclear binding energy.

Binding Energy per Nucleon (BEN)

The binding energy per nucleon (BEN), which is defined by, 

BEN = Eb / A

It is one of the most important experimental quantities in nuclear physics.

This is the average energy necessary to remove a single nucleon from a nucleus, which is comparable to the ionization energy of an electron in an atom. The nucleus is relatively stable if the BEN is reasonably large. Nuclear scattering tests are used to calculate BEN values.

Sample Problems

Problem 1: What is Mass Defect?

Solution:

The difference between the expected and actual mass of an atom’s nucleus is known as a mass defect. This discrepancy is due to the binding energy of a system manifesting as more mass.

Problem 2: Determine the Binding energy per Nucleon for a 4020Ca nucleus.

Solution:

The Total Binding energy of 4020Ca nucleus.

= 20mp + 20 mn – M ( 4020Ca)

= 20 × 1.007825 + 20 × 1.008665 – 39.962589.

= 0.367211 u = 0.367211 × 931 MeV = 341.87 Mev.

∴ Binding energy per nucleus = 341.87/40 MeV/nucleon.

= 8.55 MeV/nucleon

Problem 3: Determine the  binding energy of a nitrogen nucleus

Solution:

The nucleus of (147N) nitrogen it contains 7 protons and 7 neutrons.

mp = 1.00783 u

Mass of Neutron, mn = 1.00867

In 147N there are 7 protons and 7 neutrons,

Here, m = 14.00307 u

∴ Mass Defect, ∆m = (7mp + 7 mn) – m

= 7 × 1.00783 u + 7 × 1.00867 – 14.00307 u

= 0.11243 u

Binding energy of nucleus,

∆m × 931 MeV = 0.11243 x 931 MeV = 104.67 MeV

Problem 4: How to find the binding energy?

Solution:

The binding energy is determined by the formula:

Binding Energy = mass defect x c2

where c= speed of light in vacuum

Problem 5: Give the expression for Mass defect.

Solution:

Δm=Zmp+(A−Z)mn−mnuc

where,

Zmp is the total mass of the protons.

(A-Z)mn is the total mass of the neutrons.

mnuc is the mass of the nucleus.

 

Nuclear Force

Last Updated : 30 Mar, 2023

Nuclear forces, strong nuclear force, and weak nuclear force are two of the four fundamental forces of nature other than electromagnetic and gravitational forces. Unlike Coulomb’s Law or Newton’s Law of Gravitation, there is no simple mathematical way to describe nuclear forces. Nuclear forces are one of the strongest forces of nature.

According to the standard model nuclear forces arise due to the exchange of gluons. Since nucleons are made up of quarks, i.e., neutron (udd) and proton (uud), where u and d denote up and down quarks, respectively. The exchange of quarks between the neutron and proton keeps them intact inside the nucleus.

Fundamental Forces in Nature

There are four fundamental forces in nature which are,

• Gravitational Force
• Electromagnetic Force
• Strong Nuclear Force
• Weak Nuclear Force

Strong Nuclear Forces keep the nucleons together despite having a similar charge. Now, let’s learn about the Nuclear Force in detail in this article.

What is Nuclear Force?

The nuclear forces exist inside the nucleus, i.e., the nuclear force exists between protons and neutrons and holds them together inside the nucleus. 

Nuclear force exists between neutrons and neutrons, neutrons and protons, and protons and protons. As we know according to Coulomb’s Law same charges repel each other and protons are made of similar charges but still inside a nucleus protons are held together even though they repel each other, this is because of Nuclear force. The nuclear force is one of the strongest forces in nature hence it overcomes, the electrostatic force inside the nucleus and keeps it intact.

The nuclear forces are further classified into two categories which are discussed below,

Types of Nuclear Force

On the basis of intensity nuclear force is further classified as,

• Strong Nuclear Force
• Weak Nuclear Force

Strong Nuclear Force

Strong nuclear force is the force that acts between particles such as quarks, and other. It is the strongest force out of the four fundamental forces of interaction.  Two similar charges repel each other because of the Coulomb’s force, but in a nucleus, strong nuclear force overcomes the Colombian forces and keeps protons and protons together inside the nucleus. If the strong nuclear forces that bind protons and neutrons in an atom break, high-energy photons are released. Some of the properties of this force are,

• Strong nuclear forces are responsible for holding the nuclei of atoms stable.
• They are about 106 times greater than the weak nuclear force.
• They work at a distance of less than 10-15 m.

The magnitude of Strong Nuclear Force is far greater than the electromagnetic and gravitational force. 

Weak Nuclear Force

Weak nuclear force is involved in the particle where radioactive decay occurs. They change neutrons into protons in the process of nuclear decay. Some of the properties of this force are

• They exist between subatomic particles involving radioactive decay.
• They are neither attractive nor repulsive.

Properties of Nuclear Forces

Various properties of Nuclear forces are discussed below,

Nuclear Force is the strongest Fundamental Force

The magnitude of the nuclear force between two protons is 100 times Coulomb’s electrostatic repulsive force and 1036 times the gravitational attractive force. The nuclear force is stronger than Coulomb’s repulsive force and is able to keep the protons bound in a very small nucleus.

Nuclear force is Attractive Force

Nuclear force is attractive in nature and the variation of the potential energy of the nucleus with the distance (r) between the nucleons is shown in the figure below,

 

The graph in the figure reveals Potential energy is released at a distance of ro (≈ 0.8 fm). When the distance between two nucleons is greater than ro, the nuclear forces are attractive. As the distance between them decreases and is smaller than ro this force becomes repulsive and becomes minimum (≈ 0.8 fm) and increases rapidly which avoids the collapsing of the nucleus.

Nuclear Force is Charge Independent

The interaction between two nucleons is independent of whether one or both nucleons have a charge on them. In other words, the nuclear force between Proton-Proton (p-p)proton-neutron (p-n), and neutron-neutron (n-n)is the same, so these forces are charge independent.

Nuclear Force is Short-Range Force

The nuclear forces between two nucleons exist only when the distance between nucleons is comparable to the size of the nucleus i.e. of the order of 10-15. These forces cease to act as the distance between two nucleons exceeds 10-15. Moreover, a nucleon can interact with only its neighboring nucleons just as an atom in solid form bonds only with the surrounding atoms. Thus, these forces are short-range forces.

Nuclear Force is Exchange Force

Nuclear forces are due to the exchange of π mesons between the nucleons, so they are called exchange forces. The force between two nucleons does not act along the line joining their centers and is therefore called non-Central force.

Nuclear force is Spin-Dependent

It has been observed that the nuclear force between nucleons having parallel spins is greater than the force between nucleons having anti-parallel spins. Thus they are spin-dependent.

Examples of Nuclear Forces

As previously mentioned, the most obvious example of Nuclear Force is the binding of protons, which are naturally repulsive due to their positive charge.

• Nuclear Force is responsible for the working of the nuclear reactor and nuclear weapons.
• Strong nuclear force is responsible for the stability of the nucleus of an atom.
• Weak nuclear force is responsible for radioactive decay.

Nuclear Stability 

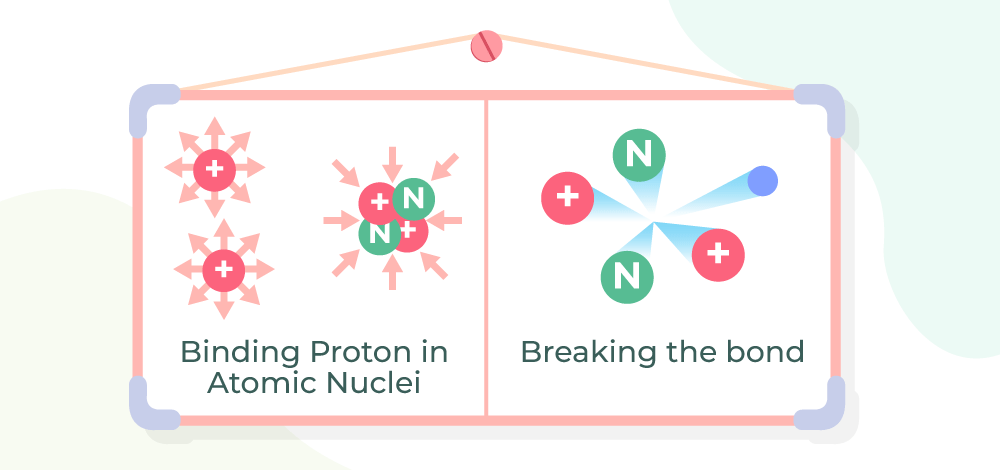
Nuclear Stability can be explained, by three forces interacting with each other inside a nucleus.

• The main force responsible for the stability of the nucleus is the Strong Nuclear Force, which is responsible for nucleus cohesiveness by pushing the different nucleons together and is also responsible for the generation of alpha radiation. 
• Electromagnetic Repulsion force acts between protons, but its magnitude is far less than the strong nuclear force.
• The third of these is the ‘weak‘ force, which works inside individual nucleons and can occasionally result in the change of a neutron into a proton (or vice versa), accompanied by the production of beta radiation.

The image shown below shows the nuclear stability and its bond breakage.

 

Read More

• Structure of Nucleus
• Fundamental Forces
• Nuclear Energy

FAQs on Nuclear Force

Question 1: What is the Nuclear Force?

Answer:

The nuclear force is the force which is responsible for the stability of the nucleus. They are the strongest fundamental forces.

Question 2: What is a Weak Nuclear Force?

Answer:

Weak nuclear forces are the forces that are responsible for the radioactive decay of the nucleus. They result in nuclear decay, such as beta decay.

Question 3: What is a strong nuclear force?

Answer:

Strong nuclear forces are the forces that are responsible for the stability of the nucleus, they are the force that acts between nucleons. They are attractive forces.

Question 4: Which of the following Particle are responsible for the Nuclear Force?

Answer:

According to the standard model gluons (exchange particles between the quarks) are the fundamental particles which are responsible for the nuclear force.

Question 5: What is the Range of Nuclear Force?

Answer:

The nuclear forces between two nucleons exist only when the distance between nucleons is comparable to the size of the nucleus, i.e., of the order of 10-15 m. These forces cease to act as the distance between two nucleons exceeds 10-15 m.

Question 6: Is Nuclear Force Charge dependent?

Answer:

The nuclear force does not depend on the charge of the particle i.e. it is independent of the charge of the particles. Thus, the force between two protons, two neutrons and one neutron and one proton is the same.

 

Radioactivity – Definition, Laws, Occurrence, Applications

Last Updated : 27 May, 2024

A nucleus is the positively charged centre of an atom made up of protons and neutrons in chemistry. The “atomic nucleus” is another name for it. The word “nucleus” is derived from the Latin nucleus, which is a derivative of the word Linux, which signifies nut or kernel.

What is Radioactivity?

The ability of certain forms of matter to emit energy and subatomic particles spontaneously is known as radioactivity. It’s essentially a property of individual atomic nuclei. 

An unstable nucleus will spontaneously dissolve, or decay, into a more stable structure, but only in a few precise ways, for as by generating specified particles or electromagnetic energy. Several naturally occurring elements, as well as artificially manufactured isotopes of the elements, have radioactive decay as a feature. The half-life of a radioactive element is the amount of time it takes for one half of any given quantity of the isotope to decay. 

Some nuclei have half-lives of more than 1024 years, while others have half-lives of less than 1023 seconds. The daughter of the parent isotope, the outcome of radioactive decay, may be unstable, in which case it will decay as well. The process continues until a stable nuclide has been formed.

Laws of Radioactivity

• The decay of the nucleus produces radioactivity.
• Temperature and pressure do not affect the rate of nucleus disintegration.
• The rule of conservation of charge governs radioactivity.
• The offspring nucleus has distinct physical and chemical properties than the mother nucleus.
• Alpha, beta, and gamma particles are always present when energy is emitted by radioactivity.
• The amount of atoms present at the time determines the rate of decay of radioactive compounds.

Alpha Decay

Alpha decay is a type of radioactive decay in which unstable atomic nuclei emit a helium nucleus (alpha particle) and transition into a more stable element in the process. The alpha particle, which was thrown out, is made up of four nucleons: two neutrons and two protons. 

The ratio of protons to neutrons in the parent nucleus is reduced by alpha radiation, resulting in a more stable structure. The nucleus of a helium atom is identical to an alpha particle. Ernest Rutherford, who employed alpha particles in his gold foil scattering experiment, conducted the first observations and investigations of alpha decay. 

The atomic number of the radioactive sample changes as the alpha particle, which is made up of two protons and a neutron, exits the nucleus. After alpha decay, the element left behind is two atomic numbers and four mass numbers smaller. For example, Uranium 23592 decays to form Thorium 23190.

Occurrence of alpha decay

Only the most massive components undergo alpha decay. The element’s nucleus should be big enough or unstable enough to undergo spontaneous fission-like modifications. In such elements, it’s the most common type of degradation. The alpha particles that are emitted from the nucleus have an energy level of roughly 5 MeV and a speed of about 5% of light. Because alpha particles lack electrons, they have a charge of +2. An alpha particle reacts violently with its surroundings due to its charge and heavy mass, quickly losing all of its energy. A few inches of air can halt their forward movement.

This type of radioactive decay reacts most aggressively with the human body due to its heaviness and charge. They have a strong ionising power, which allows them to cause havoc on tissue. The victim’s body develops blisters and burns as a result of an alpha radiation overdose.

Applications of radioactivity

• The alpha emitter americium-241 is utilized in household smoke detectors in the United States.
• The alpha particles emitted by the Americium sample ionize the air in the smoke detector chamber, causing a small current to flow.
• When smoke enters the chamber, it produces a current drop, which sets off the alarm. Although Alpha particles have a very low range, they are extremely lethal when they come into contact with each other.
• When eaten, alpha emitters come into intimate contact with tissue and are lethal in such situations, and are thus employed in assassination attempts through radiation poisoning.

Advantages and Disadvantages of Radioactivity

Advantages of radioactivity are:

• Gamma rays are employed in radiotherapy to eliminate malignant cells.
• Cobalt-60 is used to kill cancer-causing cells.
• The interior regions of the body are scanned with gamma rays.
• Gamma rays kill bacteria in food and extend its shelf life by preventing deterioration.
• The age of the rocks can be determined using radioactive radiations and the amount of argon present in the rock.

Disadvantages of radioactivity are:

• The effects of a high dose of radioactive radiation on the body could be fatal.
• The cost of radioactive isotopes is high.

Sample Problems 

Problem 1: Write the alpha-decay reaction for Cf−246?

Solution:

The helium atom, with atomic number 2 and atomic mass number 4, is lost by the radioactive atom. The radioactive atom is transferred to an atom with a two-digit atomic number and a four-digit atomic mass.

The unbalanced equation,

24698Cf → 42He + X

The superscript of X is :
246−4 = 242

The subscript of X is:
98−2 = 96

Thus, the X has the atomic number 96.

The element with the atomic number 96 is curium (Cm).

So, the alpha-decay equation for Cf -246 is:

24698Cf → 24296Cm + 42He

Problem 2: What are the uses of radioactivity?

Solution: 

• Smoke detectors in the home are made of this material.
• Sterilization of medical instruments
• It’s a tool that’s used to diagnose and cure ailments.
• It is used to generate electricity

Problem 3: What are the units of radioactivity? 

Solution:

Curie and Rutherford are the units of radioactivity.

1C = 3.7 × 104 Rd is the relationship between Curie and Rutherford.

Problem 4:  Which elements can undergo alpha decay?

Solution:

Alpha decay can occur in any element heavier than lead. Lighter elements, on the other hand, show no signs of radioactive decay. Alpha decay is a typical phenomenon in heavier elements than bismuth, which has an atomic number of 83. Alpha decay can also be seen in rare earth elements such as neodymium, which has an atomic number of 60, and lutetium, which has an atomic number of 71.

Problem 5: A stationary uranium nucleus scatters an α-particle with an energy of 5 MeV through 180°.What is the order of the distance of the closest approach ? 

Solution

Distance of closest approach :−

r0 = ze 2e/4π∈0E

KE=PE

1/2mv2 = 1/4π∈0  x  q1q2/r​

r = 9×109×2×92×(1.6×10−19)2/5×106×1.6×10−19

= 5.3×10−14m

≈5.3 x 10−12cm

 

Nuclear Energy – Definition, Types, Applications

Last Updated : 25 Feb, 2024

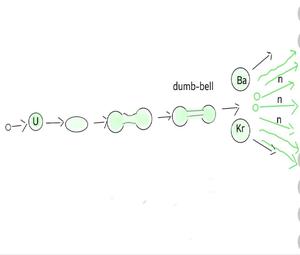
Nuclear energy, also known as atomic energy, is the energy released in large quantities by operations that influence atomic nuclei, the dense centres of atoms. It differs from the energy of other atomic phenomena like typical chemical reactions, which solely involve atoms’ orbital electrons. Controlled nuclear fission in reactors, which are currently used to generate electricity in many parts of the globe, is one means of releasing nuclear energy. Controlled nuclear fusion, another way for getting nuclear energy, has shown promise but will not be achieved by 2020. Nuclear fusion and nuclear fission have both released massive amounts of nuclear energy.

Nuclear Energy 

The energy obtained from the conversion of nuclear mass is known as nuclear energy. Binding energy per nucleon of light nuclei and heavy nuclei is small as compared to the binding energy per nucleon of intermediate nuclei. 

When a heavy nucleus splits into two lighter nuclei then the binding energy per nucleon of light and nuclei is more than the binding energy per nucleon of the original heavy nucleus. Thus large energy is released in the process of splitting the nucleus. This process is known as nuclear fission. 

For example, 1 kg of Uranium on fission gives 1014 J of energy whereas 1 kg of coal on burning gives 107 J of energy. On the other hand, when two light nuclei fuse or combine together to form a relatively heavy nucleus then the binding energy per nucleon increases. Large energy is released in the process known as nuclear fusion.

Nuclear Reactions 

Atomic nuclei undergo changes as a result of nuclear reactions, which result in changes in the atom itself. Nuclear reactions change one element into something wholly other. 

If a nucleus interacts with other particles and then separates without changing the properties of other nuclei, the process is referred to be nuclear scattering rather than a nuclear reaction. This has nothing to do with radioactive decay. Nuclear fusion, which happens in fissionable materials and results in induced nuclear fission, is one of the most visible nuclear reactions.

Types of Nuclear Reactions 

• Inelastic scattering: When energy is transferred, this phenomenon is called inelastic scattering. It happens when the energy level is higher than the threshold. i.e.

Et = ((A+1)/A)× ε1

where Et is the inelastic threshold energy and ε1 is the first excited state’s energy.

• Elastic Scattering: Elastic Scattering happens when energy is transferred from a particle to its intended nucleus. It’s the most important step in slowing down neutrons. The entire kinetic energy of any system is preserved in the event of elastic scattering.
• Transfer Reactions: Transfer reactions are defined as the absorption of a particle followed by the emission of one or two particles.
• Capture Reactions: Capture reactions occur when nuclei capture neutral or charged particles followed by the emission of -rays. Neutron capture processes create radioactive nuclides.

Why Nuclear fusion is known as a thermonuclear reaction

Nuclear fusion cannot take place so easily. When two light nuclei are brought closer to each other, they exert a repulsive force on each other due to their positive charges. As such, these nuclei cannot fuse together. These nuclei confuse together if they have enough kinetic energy to overcome the force of repulsion between them. High kinetic energy implies a high temperature. Thus, nuclear fusion can be achieved at a very high temperature and hence is known as a thermonuclear fusion reaction. in fact, the temperature of the order of 107 K is required to trigger nuclear fusion. This much temperature is available in the core of the sun and other stars, so nuclear fusion is possible in the sun and other stars.

Applications of Nuclear Energy 

• Fissionable material (Fuel): The fissionable material used in the reactor is called the fuel of the reactor. Uranium isotope(U235), Thorium isotope (Th232) and plutonium isotopes(Pu239, Pu240 and Pu241) are the most commonly used fuel in the reactor.
• Moderator: Moderator is used to slow down The fast-moving neutrons. The most commonly used moderators are graphite, water and heavy water. when heavy water is used as a moderator, then ordinary or non-enriched uranium can be used as a fuel because heavy water has more neutrons to produce fission. In the case of ordinary water as a moderator(having few electrons) enriched Uranium is used as a fuel.
• Control Material: control material is used to control the chain reaction and to maintain a stable rate of reaction. This material controls the number of neutrons available for fission. For example, cadmium rods are inserted into the core of the reactor because they can observe the neutrons. The neutrons available for fission are controlled by moving the cadmium rods in or out of the core of the reactor.
• Coolant: Coolant is a cooling material that removes the heat generated due to fission in the reactor. Commonly used coolants are water, CO2 nitrogen etc.
• Protective Shield: A protective shield in the form of a concrete thick wall surrounds the core of the reactor to save the persons working around the reactor from hazardous radiations.

Sample Problems

Question 1: Calculate the energy released in the following reaction:

3Li6 + 0n1 ⇢2He4 + 1H3

where Mass of 3Li6 =6.015126amu, Mass of 1H3 =3.016049amu, Mass of 2He4 =4.002604 amu, Mass of 0n1 =1.008665 amu.

Answer:

Total mass of reactants = 6.015126 + 1.008665 = 7.023791 amu

Total mass of products = 4.002604 + 3.016049 = 7.018653 amu

Mass difference = (7.023791 – 7.018653) = 0.005138 amu

Energy released = 0.005138 × 931  MeV = 4.783MeV.

Question 2: The nucleus of an atom is 92Y235 initially at rest, decays by emitting on α particle as per the equation:

92Y235 ⇢90X231 + 2He4 + Energy 

It is given that the binding energies per nucleon of the parent and the daughter nuclei are 7.8 MeV and 7.835MeV respectively and that of α particle is 7.07 MeV/nucleon.  Assuming the daughter nucleus to be formed in the unexcited state and neglecting its share in the energy of the reaction. Calculate the speed of the emitted α particle. Take the mass of α particle to be 6.68 × 10 -27 kg.

Answer:

Q = (7.835 ×231) + (7.07 × 4) – (7.8 × 235 )MeV

   = 5.18 MeV

   = 5.18 ×1.6 ×10-13J

This entire kinetic energy is taken by  α particle as given

1/2 mv2 = 5.18 × 1.6×10-13

1/2 × 6.68 ×10-27 v2 = 5.18 × 1.6 ×10-13

v = 1.57 × 107 m/s.

Question 3: Is the fission of iron(26Fe56) into aluminium(13Al28) As given below is possible?

26Fe56 ⇢13Al28 +13Al28 +Q

Given, Mass of 26Fe56 =55.934940u and mass of 13Al28 =27.98191 u.

Answer:

Q value =mass of 26Fe56 – 2 ×mass of 13Al28 

              = (55.934940 – 2 ×27.98191) ×931.5 MeV/u

             = -0.02892u × 931.5 MeV/u

             = -26.94 MeV. 

Question 4: 20 MeV energy is released per fusion reaction

1H2 +1H2 ⇢ 2He4 +0n1

Calculate the mass of 1H2 consumed in a fusion reactor of power 1 MW in 1 day.

Answer:

P =1 MW =106 W =106 Js-1

t =1 day  =24 × 60 × 60 = 86400 s

Energy released in 1 day = 86400× 106 J

Energy released per fusion = 20MeV

                                           = 20 × 1.6 ×10-13 = 3.2 × 10-12 J

Mass of 1H2 consumed in one fusion (1H2 + 1H2) = 4u

                                                                              = 4 ×1.66 ×10-27 kg = 6.64 ×10-27

                                                                              = 6.64 × 10-27/ 3.2 × 10-12 × 86400 ×106

                                                                             = 1.79 × 10-4 kg

Question 5: Calculate the energy released when three α particles (2He4) fuse to form a carbon (6C12) nucleus, given m (2He4) = 4.002603 amu.

Solution:

2He4 ⇢ 6C12 +Q

Q = m(3 2He4) – m(6C12)

   = 12.0078 – 12 = 0.007809

Energy released = 0.007809 × 931 MeV

                          = 7.27MeV